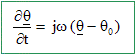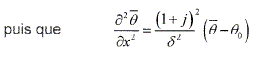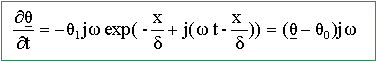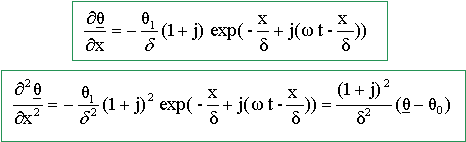Géothermie : diffusion de la chaleur ; pompe à chaleur ; calcul de la résistance thermique d'un matériau Concours Caplp externe 2008

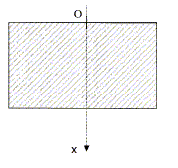
Diffusion de la chaleur. Répercussion en profondeur des variations de température annuelle au niveau du sol. On assimile l'écorce terrestre, localement, à un demi-plan positif infini situé du coté des x positifs. On considère le sol de masse volumique m constante, de chaleur massique c et de conductivité thermique K. On appelle q(x,t) la répartition de température en régime permanent en fonction de la profondeur et du temps. La loi régissant l'équation de propagation de la chaleur est : Quel nom porte cette loi ? Loi de Fourier. On cherche une solution à cette équation de la forme suivante : q(x, t) = q 0-q1 exp(-x/d) cos (wt-x/d) où d est une constante positive réelle. On pourra utiliser la notation complexe : q(x, t) = q 0-q1 exp[-x/d +j(wt-x/d)] avec j2=-1. Montrer que q(x, t) = Re(q(x, t)). exp(j(wt-x/d))= cos(wt-x/d) + j sin (wt-x/d) ; q(x, t) = q 0-q1 exp(-x/d ) [cos(wt-x/d) + j sin (wt-x/d)] Re(q(x, t)) = q 0-q1 exp(-x/d ) cos(wt-x/d). 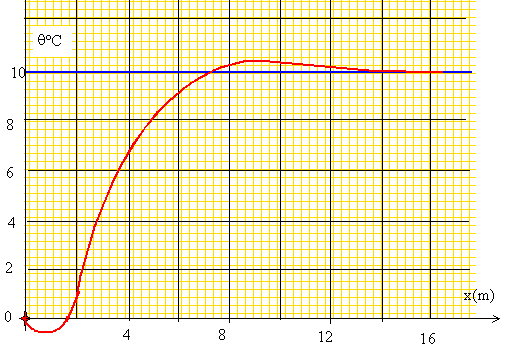Montrer que :   En déduire que q est solution de l'équation de propagation (1) si et seulement si : d2=2K / (mcw). Repport dans (1) : mc(q-q0)jw -K(1+j)2/d2 (q-q0) =0 mcjwd2-K(1+j)2 =0 ; j mcwd2-K(1+2j+j2) =0 ; j(mcwd2-2K)=0 cette égalité est vérifiée si : mcwd2=2K d2=2K / (mcw).   Epaisseur de peau. En procédant à une étude dimensionnelle, montrer que d a la dimension d'une distance. En fait d est appelé épaisseur de peau. K ; : conductivité thermique en W m-1 K-1 ou J s-1 m-1 K-1 m masse volumique en kg m-3 ; c : chaleur massique en J kg-1 K-1 ; w : pulsation en rad s-1. mcw en : J s-1 m-3 K-1 ; d2 en m2 ; d en mètre. Calculer la période T puis la pulsation w. T = 365 jours = 365*24*3600 s = 3,15 107 s ; w = 2p/T = 6,28 / 3,15 107 =2,0 10-7 rad/s. Calculer d. m = 3,00 103 kg m-3 ; c= 515 J kg-1K-1 ; K = 1,00 J m-1 s-1 K-1. d2=2K / (mcw) = 2 /(3,00 103*515*2,0 10-7) =6,50 ; d=6,5½ = 2,55 m. Température minimale au 1er janvier : qm = -10 °C ; température maximale au 1er juillet : qM= 30 °C. Montrer que q0 = ½(qm +qM) etq0 = ½(qM -qm) puis calculer ces valeurs. Pour x=0 et t=0 ( 1er janvier) : q(0,0) = q0-q1 = qm (2). Pour x=0 et t=½T ( 1er juillet) : q(0,½T) = q0-q1cos p =q0+q1 = qM (3). (2)+ (3) donne : q0=½(qm+qM )=10°C ; (3)- (2) donne : q1=½(qM-qm )=20°C.   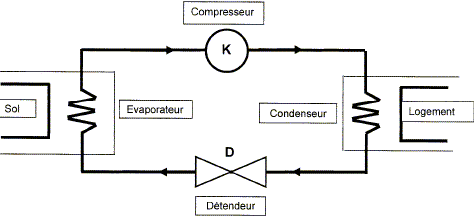Pour quelle date, notée t0, la température est-elle minimale à une profondeur de 2 m , Calculer cette valeur minimale. Rechercher la valeur du temps qui annule la dérivée de q(2,t) par rapport au temps : dq(2,t) /dt = -q1 exp(-2/2,55) (-w)sin(wt0-2/2,55) =0 ; sin(wt0-2/2,55) =0 wt0-2/2,55=0 ; t0=2/(2,55w) = 2/(2,55*2,0 10-7) =3,92 106 s = 45,4 jours ( 15 février ). Tracer la courbe q(x, t1) pour une date t1 correspondant au 1er mars. t1= 2 mois = T/6 ; wt1 = p /3 ; q(x,t1) = 10-20 exp(-x/2,55) cos(p /3- x/2,55). x(m) 0 0,5 1 1,5 2 3 4 5 8 10 12 15 q(x,t1) °C -0,1 -0,9 -0,76 0 1,2 3,9 6,7 8,3 10,4 10,4 10,2 10 Dans le cas d'un matériau homogène et isotrope, sans perte thermique à la surface du matériau, la quantité de chaleur trnsmise par conduction thermique à travers une paroi d'épaisseur L pendant une durée Dt est : Q = l S Dq D t / L avec : l : coefficient de conduction thermique W m-1 K-1. S : section de la surface d'échange m2. Dq : variation de la température . Donner l'expression du flux thermique F en fonction de l ,S, Dq et L. F =Q /D t= l/ L S Dq Une autre expression du flux thermique est F = SDq / R, avec R la résistance thermique. Donner l'expression et l'unité de la résistance thermique. R = L/ l : L en mètre ; l en W m-1 K-1 ; R en W-1 m2 K. Calculer la résistance thermique d'un mur de béton armé d'épaisseur 15 cm, de surface 17 m2, de température superficielle intérieure 20°C et de température superficielle extérieure -4°C : Coefficient de conductivité thermique du béton l = 1,75 W m-1 K-1. Rbéton = 0,15 / 1,75 = 0,086 W-1 m2 K. Pour renforcer l'isolation thermique de ce mur, deux solutions sont envisagées : Solution 1 : Ajouter une plaque de platre de 13 mm d'épaisseur et de conductivité thermique 0,35 W m-1 K-1 accolée à une plaque de polystyrène de 70 mm d'épaisseur et de conductivité 0,037 W m-1 K-1.  Solution 2 : Ajouter une cloison de brique d'épaisseur 50 mm et de conductivité 1,15 W m-1 K-1 séparée du mur par une couche d'air de 20 mm d'épaisseur et de conductivité 0,023 W m-1 K-1. Déterminer la solution qui représente la meilleure isolation. La résistance thermique d'une paroi est la somme des résistances thermiques des différentes couches qui la constituent. Solution 1 : Rplatre = 0,013/0,35 = 0,037 W-1 m2 K ; Rpolystyrène = 0,070/0,037 = 1,89 W-1 m2 K. Rbéton + Rplatre +Rpolystyrène = 2,0 W-1 m2 K. Solution 2 : Rbrique = 0,050/1,15 = 0,043 W-1 m2 K ; Rair = 0,020/0,023 = 0,87 W-1 m2 K. Rbéton + Rbrique +Rair = 1,0 W-1 m2 K. La solution 1 correspondant à la meilleure résistance thermique est retenue. 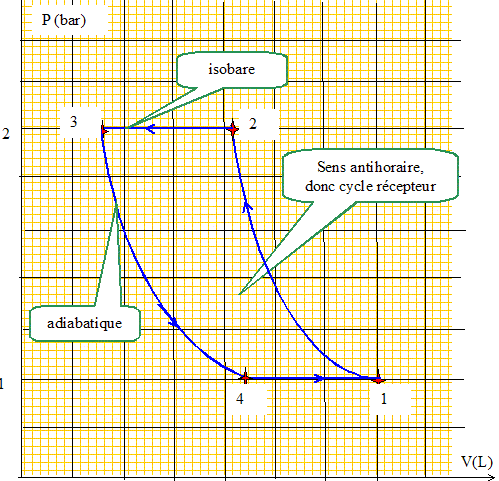Pompe à chaleur : La pompe géothermique est une machine thermodynamique constituée d'un circuit fermé et étanche dans lequel circule un fluide frigorigène qui subit un changement d'état. Le schéma de principe de la pompe à chaleur est le suivant : Evaporateur : au contact de la chaleur puisée dans le sol, le fluide frigorigène liquide, se transforme en vapeur. Compresseur : cette vapeur est portée à haute pression. Condenseur : le liquide frigorigène transmet sa chaleur au circuit de chauffage du logement. Le fluide frigorigène toujours comprimé devient liquide. Détendeur : la pression du fluide frigorigène est réduite. Il est prêt à une nouvelle absorption de chaleur provenant du sous-sol. Comment s'effectue le transfert de chaleur entre deux corps ? Citer deux mode de propagation de la chaleur. Transfert par conduction, convexion et rayonnement. Indiquer deux effets possibles de la chaleur. Elévation de la température d'un corps sans changement d'état physique. Changement d'état physique d'un corps. Nommer le changement d'état subit par le fluide dans le condenseur. La vapeur se liquéfie : liquéfaction. Identifier la source chaude et la source froide dans le fonctionnement de la pompe à chaleur. La source chaude reçoit de la chaleur : c'est le local à chauffer. La source froide cède de la chaleur au fluide : c'est le sous sol. Où la pression est-elle la plus basse ? Où est-elle la plus élevée ? Pression élevée à la sortie du compresseur ; pression la plus faible à la sortie du détendeur.   La pompe à chaleur fonctionne donc entre 2 sources. Le fluide frigorigène utilisé dans le circuit fermé sera assimilé à un gaz parfait de capacité thermique molaire cp=29,1 J K-1 mol-1. g = 1,4. Le fluide décrit le cycle thermique suivant : Dans le compresseur : compression adiabatique, la pression passe de p1=105 Pa à p2 = 2 105 Pa ; la température passe de T1 = 310 K à T2. Dans le condenseur : refroidissement isobare ; la température passe de T2 à T3 = 330 K. Dans le détendeur : détente adiabatique, la pression passe de p3= 2105 Pa à p4 =p1= 105 Pa ; la température passe de T3 à T4 = 271 K. Dans l'évaporateur : échauffement isobare jusqu'à la température passe de T1. Représenter l'allure du cycle dans le diagramme de Clapeyron ( p, V). Indiquer par des flèches le sens des transformations. Définir une transformation adiabatique. Le système n'échange pas de chaleur avec l'extérieur. On donne l'expression de la quantité de chaleur dQ échangée avec l'extérieur par n moles de gaz parfait, au cours d'une transformation quasi-statique élémentaire quelconque : dQ = 1/(g-1) (g P dV + VdP). Retrouver l'expression de la loi de Laplace PVg=Cte dans le cadre d'une adiabatique réversible. dQ =0 donc g P dV + VdP=0 ; g dV/V=-dP/P : g d ln V = -d ln P ; g ln V = -lnP + Cste g ln V +lnP + Cste ; ln Vg +lnP + Cste ; PVg = constante. Montrer que T2 = 378 K. PVg = constante ; Or V = nRT/P d'où : P1-gTg = constante. P11-gT1g =P21-gT2g ; T2 = T1[P1/P2](1-g)/g ; T2 =310*0,5-0,286 = 378 K Calculer les quantités de chaleur échangées par une mole de fluide frigorigène au cours de chacune des 4 transformations. On note Qc la quantité de chaleur échangée au contact de la source chaude et Qf la quantité de chaleur échangée au contact de la source froide. Lors des transformations adiabatiques : Q12 = Q34=0. Lors des transformations isobares : Q = Cp(Tf-Ti) ; Q23 = Qc =Cp(T3-T2) =29,1(330-378) = -1397 J mol-1. Q41 = Qf =Cp(T1-T42) =29,1(310-271) = 1135 J mol-1. Quelle est la variation de l'énergie interne du fluide qui décrit un cycle ? DUcycle = 0 (même état initial et final) Enoncer le premier principe de la thermodynamique pour un cycle. DUcycle = W + Qf + Qc =0 En déduire le travail W reçu par une mole de fluide au cours d'un cycle. W = - Qf - Qc =-1135 + 1397 = 262 J mol-1. L'efficacité de la pompe à chaleur est le rapport de la quantité de chaleur recherchée par l'emploi de la pompe à chaleur au cours du cycle au travail reçu par le fluide au cours du même cycle. Dans le cas de la pompe à chaleur, quelle est la quantité de chaleur recherchée ? Chaleur cédée au local. Donner l'expression de l'efficacité e et la calculer. e= -Qc/W = 1397/262 = 5,3. Proposer une signification de cette valeur. L'eficacité n'est pas un rendement ; c'est la chaleur cédée au local à chauffer par rapport au travail investi.

retour -menu