Acoustique : onde sonore ; émission, propagation, réception Concours Caplp externe 2008

Production d'un son. Indiquer la diférence entre un bruit et un son musical. Un son musical est un son possédant une hauteur fixe ; il est caractérisé par son timbre.On le symbolise par une note. Bruit : toute sensation auditive désagréable et génante. C'est une vibration de l'air qui se propage. Citer deux sources émettrices de sons musicaux. Vibration d'une corde de guitare ; vibration d'une fine lame de bois fixée sur le bec dans une clarinette. Citer deux sources émettrices de bruit ou sons non musicaux. Lame, corde vibrante ; dans le cas instruments " les cuivres" , les vibrations sont produites au niveau de l'embouchure : l'air y est injecté par bouffées conduisant à une série de tourbillons. Les 3 qualités physiologiques des sons musicaux sont la hauteur, l'intensité et le timbre.  Préciser ce que chacune de ces qualités permet de distinguer et indiquer ce qui la caractérise. Une note de musique est caractérisée par sa hauteur, grandeur liée à la fréquence fondamentale du son qu'elle représente.   A hauteur identique, les sons émis par deux instruments différents ne résonnent pas de la même manière. Le timbre résulte de la combinaison d'un son fondamental et de ses harmoniques. Intensité d'un son : amplitude de la vibration, qui se mesure en décibels. Dans le cas d'un son complexe, définir le fondamental et les harmoniques. Le fondamental est l'harmonique de rang 1. Les harmoniques d'un son musical ont des fréquences multiples de celle du fondamental. Définir un son simple ou son pur ? Préciser la nature de la vibration. Son pur : une seul fréquence ( exemple du la3 du diapason) ; la vibration est sinusoïdale. Propagation d'un son : Décrire une expérience simple permettant de mettre en évidence la nécessité d'un milieu matériel pour qu'un son puisse se propager. Faire sonner un réveil dans une chloche à vide dans laquelle on a retiré l'air : aucun son n'est perçu.   On considère un tube cylindrique rectiligne contenant de l'air à l'entrée duquel on place une lame vibrante émettant un son. Réaliser un ou plusieur(s) schéma(s) et expliquer comment le son se propage dans le tube, en précisant la grandeur physique qui permet cette propagation. Un modèle permettant d'étudier la propagation des sons consiste à découper le milieu de propagation en tranches identiques susceptibles de se comprimer et de se détendre. On fait correspondre à chaque tranche un chariot et un ressort. Une brève impulsion sur le premier chariot permet de simuler la propagation d'une onde progressive longitudinale : propagation d'une variation de pression. Une onde sonore est caractérisée par deux périodicités. Nommer et expliquer ces deux périodicités. Période temporelle T = 1/ f ( exprimée en seconde) Période spatiale ou longueur d'onde l (m) : l = cT La longueur d'onde est la distance entre deux points consécutifs se trouvant dans le même état vibratoire. Définir la longueur d'onde sonore à partir de l'expression de la viration en un point de l'espace ? Deux points se trouvant dans le même état vibratoire ( en phase) sont distants d'un nombre entier de longueur d'onde. Donner l'expression de la célérité d'une onde. c = l f avec l : longueur d'onde (m) et f : fréquence (Hz) Proposer un montage expérimental permettant de déterminer la célérité d'une onde sonore. A.N : f= 2000 Hz ; milieu de propagation : l'air ; c= 340 m/s ; calculer la période T et la longueur d'onde l. T = 1/f = 1/2000 = 5 10-4 s. l =c/f = 340/2000 = 0,17 m.   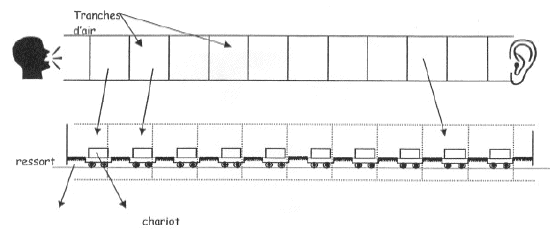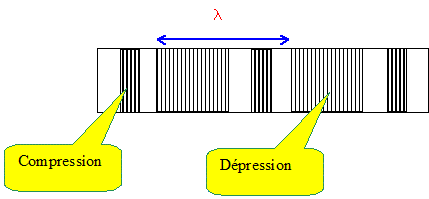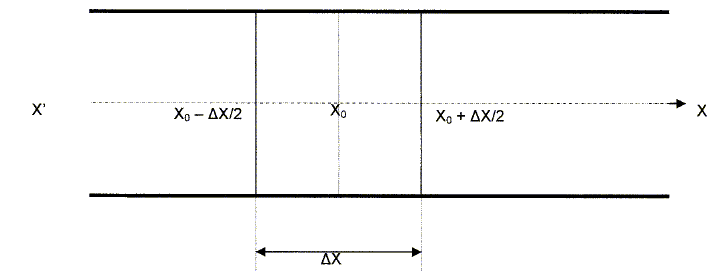Dans cette question, on se limite au cas particulier des ondes acoustiques planes se propageant dans un milieu homogène et compressible suivant une direction x'x. Pour cela, on étudie les variations de volume et de pression d'un gaz emprisonné dans un tuyau droit de section S lorsqu'une onde acoustique se propage dans le tuyau. Dans l'étude suivante, on considère une tranche de gaz centrée au point x0. La propagation des ondes sonores dans les gaz est en général un processus adiabatique. Dans ces conditions on peut écrire PVg=Cte.(1) g est le rapport de la chaleur massique à presion constante sur la chaleur massique à volume constant. On appliquera la théorie des gaz parfaits à la tranche de gaz considérée. La température absolue à l'équilibre sera notée T0 et la pression à l'équilibre sera notée P0. Prende la différentielle logarithmique de (1) et exprimer en fonction de g et P0 le coefficient de compressibilité isotherme c( en Pa-1) est défini par : c=-1/V . DV/DP. log P + g log V = log Cte ; dP/P + g dV/V = 0 ; -g dV/V = dP/P ; -dV/dP = V/ (gP) ; -1/V. dV/dP =1/ (gP). c=1/ (gP). La réponse à la question précédente permet d'exprimer la vitesse v du son dans un gaz parfait par v = [gP0 /r0]½,(2) lorsque r0 est la masse volumique du gaz. Exprimer la vitesse v en fonction de g, R, T0 et M( masse molaire du gaz).  Loi des gaz parfaits : PV = nRT avec n = masse / masse molaire ; n = m/M et masse volumique r = m/V. P = mRT/(VM) = m/V. RT/M = r RT/M ; P/r = RT/M Repport dans (2) : v= [gRT/M]½ . A.N : calculer la vitesse du son dans l'air à la température de 20°C. M = 29 g/mol. T = 273+20 = 293 K ; M= 0,029 kg ; R= 8,32 J mol-1K-1 ; g=1,4. v = [1,4*8,31*293/0,029]½ =343 m/s. Réception d'un son. 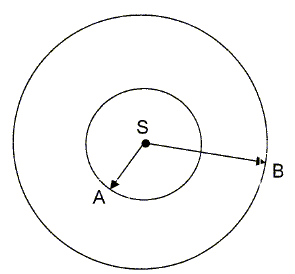Soit une source S, considérée comme ponctuelle, qui émet un son. On appelle puissance acoustique la puissance P(watt) rayonnée dans l'air par une source S sous forme d'une onde sonore. L'air étant assimilé à un milieu élastique homogène et isotrope, les surfaces d'onde sont donc des sphères concentriques de centre S. On appelle intensité acoustique notée I et exprimée en W m-2, la puissance acoustique qui traverse une unité de surface. On considère deux surfaces d'onde de rayons respectifs r1 et r2 avec r1<r2. Exprimer en fonction de r1 et r2, le rapport IA/IB des intensités acoustiques IA en A et IB en B. P : puissance acoustique de la source sonore. P = IA.4pr12 ; P = IB.4pr22 ; IA/IB = r22/ r12 =(r2/r1)2. A une distance d1 = 2 m d'une pompe à chaleur ( source émettrice d'un son), l'intensité acoustique est I1 = 10-4 W m-2. Calculer l'intensité acoustique I2 à une distance d2 = 10 m de cette même pompe. I2 = I1 (d1/d2)2 = 10-4*0,22 = 4 10-6 W m-2. En déduire le niveau acoustique L à cette distance de 10 m. I0 = 10-12 W m-2. L = 10 log(I2/I0) = 10 log (4 10-6 /10-12 ) = 66 dB.  On souhaite que le niveau d'intensité acoustique ne dépasse pas 30 dB à 10 m de la source. Quelle doit être la puissance acoustique maximale PM du son émis par la pompe ? PM = 4pId2 ;  I = I0 10L/10 = 10-12 * 103 = 10-9 W m-2. PM = 4*3,14*10-9 *100 = 1,3 10-6 W. 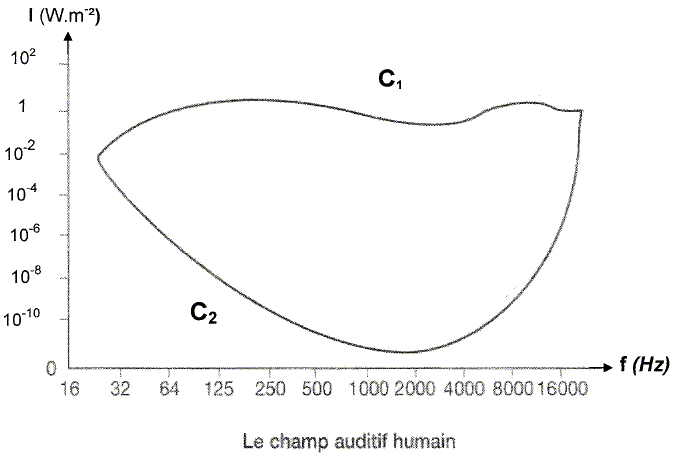Perception d'un son : Chez l'homme, l'oreille est l'organe de perception des sons. Le diagramme ci-dessous donne les variations de l'intensité acoustique I en fonction de la fréquence f (Hz) des sons perçus ; ces courbes définissent le champ auditif humain. 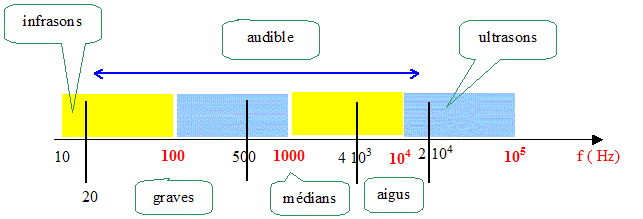A partir du diagramme donné : Situé sur un axe gradué de façon logarithmique en fréquence, les zones correspondant aux infrasons, aux ultrasons et au domaine de l'audiilité. Pour le domaine de l'audiilité, situer la zone correspondant aux sons aigus, aux sons médium et aux sons graves.   Préciser à quoi correspondent les courbes C1 et C2. Quels noms portent ces courbes ?  C1 : seuil de la douleur ; C2 seuil d'audibilité. La valeur de l'intensité acoustique de référence est I0 = 10-12 W m-2. Préciser à quoi correspond cette valeur et, à partir du diagramme, justifier ce choix. La sensibilité de l'oreille est maximale vers 1000 Hz. Si on se situe uniquement dans la zone des sons graves, cette valeur retenue pour I0 est-elle encore justifiée ? Pourquoi ? La sensibilité de l'oreille diminue dans le domaine des sons graves ( 20 Hz < f < 500 Hz). On assimile l'oreille humaine à une surface d'aire S= 0,6 10-5 m2. 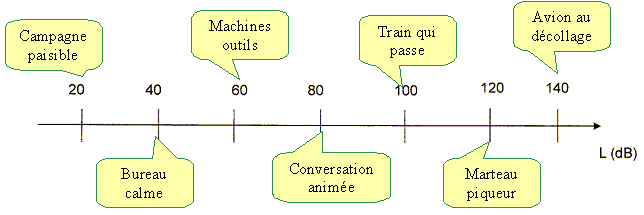Calculer l'énergie reçue par cette oreille en une journée si le niveau d'intensité acoustique est constant et égal à 30 dB. Intensité acoustique  I = I0 10L/10 = 10-12 * 103 = 10-9 W m-2. Puissance acoustique de la source : PM =I . S =10-9 *0,6 10-5 = 6 10-15 W. Dt=1 jour = 24*3600 =8,64 104 s ; Energie = PM*Dt =6 10-15* 8,64 104 =5,2 10-10 J. Indiquer la forme des pavillons des appareils porte-voix et sonotone. Préciser pour quelle raison ces appareils ont leur efficacité. Le pavillon est évasé : on atténue la dispersion de la surface d'onde ; on amplifie le son de la voix. Reproduire l'axe gradué ci-dessous en associant aux bruits de la liste suivante les valeurs des niveaux d'intensité acoustique indiqués : machines rotatives d'outillage - campagne paisible - passage d'un train en gare - petit bureau calme - marteau piqueur - conversation animée - avion au décollage.

retour -menu