système triphasé : montage étoile ; montage triangle concours Caplp interne 2008

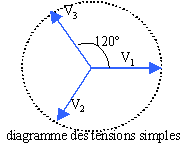
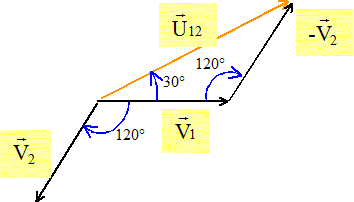
Tensions simples. Un système triphasé équilibré est constitué de trois tensions simples sinusoïdales, de même fréquence, de même valeur efficace et déphasées l'une par rapport à l'autre de 2p/3 rad. Soit v1, v2 et v3 les trois tensions simples entre le neutre et chacune des phases. L'expression de v1 est v1 = V 2½ sin (wt) Préciser la nature des grandeurs physiques symbolisées par V, w et t. Donner les unités. V : tension efficace (volt) ; t : temps en seconde ; w : pulsation en rad/s. Exprimer la fréquence f en fonction de w. w =2pf ; f =w /(2p ) pulsation en rad/s ; f : fréquence en hertz. Donner les expressions de v2 et v3 en fonction de V, w et t. v2= V 2½ sin (wt- 2p/3) ; v3= V 2½ sin (wt+ 2p/3) Les vecteurs sont écrits en gras et en bleu. Représenter sur un diagramme les vecteurs de Fresnel V1, V2 et V3 associés à v1, v2 et v3. Dans un établissement, les élèves disposent uniquement d'une source triphasée très basse tension et d'un oscilloscope bicourbe. 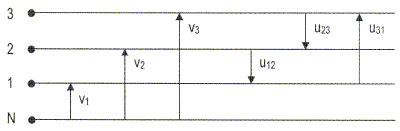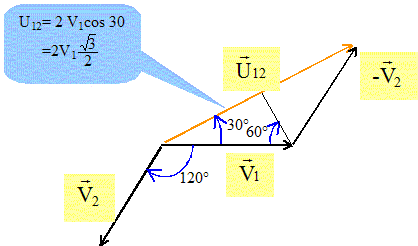Indiquer un protocole expérimental permettant de visualiser les tensions simples et de mesurer leurs déphasages. Indiquer un schéma de branchement.  V1+ V2= -V3 On réalise un montage afin de visualiser v1 et v2 sur les deux voies de l'oscilloscope ( neutre relié à la masse ) : on visualisera v3 en additionnant les signaux sur les deux voies ( bouton ADD) puis en prenant l'opposé ( bouton INV). Déphasage : fréquence 50 Hz ; période T = 20 ms soit 2p radians ; 10 divisions sur l'axe horizontal ; sensibilité choisie : 2 ms/div soit 2p/10 rad par division. déphasage entre deux tensions : 3,3 divisions. Tensions composées. Les tensions composées u12, u23, u31 sont les tensions entre deux phases respectives. Elles sont liées aux tensions simples par les expressions : u12= v1-v2 ; u23= v2-v3 ; u31= v3-v1. Construire sur le diagramme précédent les vecteurs U12, U23 et U31 associés à ces tensions. Déterminer la mesure de l'angle (V1, U12 ).   Montrer que la relation entre les valeurs efficaces des tensions simples et composées s'écrit : U = 3½ V.   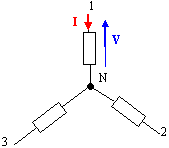Montage étoile. On désire brancher en étoile avec neutre 3 dipôles résistifs de résistance R=46 W aux bornes d'un générateur triphasé donc chaque tension simple a pour valeur V=230 V. Proposer un schéma de câblage de ces trois dipôles. 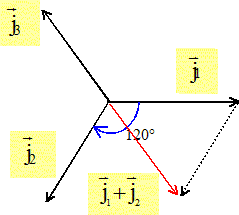Calculer les intensités des courants dans les fils de phase et, éventuellement, dans le fil de neutre. Représenter le diagramme de Fresnel associé. Chaque impédance est alimentée sous une tension simple ; l'intensité du courant dans un fil de ligne est égale à l'intensité du courant dans une impédance. Si les trois impédances sont identiques le montage est dit équilibré et le courant dans le fil neutre est nul. J = V/R = 230/46 = 5 A. Calculer la puissance électrique absorbée par l'ensemble de ces trois dipôles. P = U I 3½ cos j avec cos j = 1 ; I= 5 A (intensité en ligne) et U = V 3½ ( tension composée) P = 230*5*3 = 3450 W. Le fil de neutre est coupé. Déterminer les intensités des courants dans les fils de phase. Identique au calcul ci-dessus : dans un montage étoile équilibré le neutre n'est parcouru par aucun courant. Le fil de neutre est cablé ; la résistance branchée à la phase 1 est accidentellement déconnectée. Déterminer les intensités des courants dans les fils de phase et, éventuellement, dans le neutre. intensité dans chaque phase : 5 A ; intensité dans le neutre 5 A. 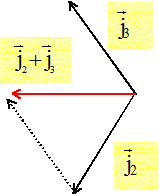Le fil de neutre est coupé ; la résistance branchée à la phase 1 est accidentellement déconnectée. Déterminer les intensités des courants dans les fils de phase. Les fils de phase 2 et 3 sont traversés par l'intensité : I= U/(2R) = 230 * 3½ / (2*46) =4,33 A. 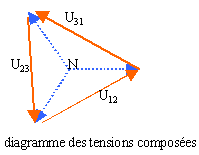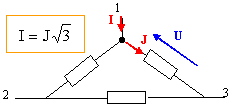Montage triangle. On désire brancher en triangle 3 dipôles résistifs de résistance R=46 W aux bornes d'un générateur triphasé donc chaque tension simple a pour valeur V=230 V. Proposer un schéma de câblage de ces trois dipôles. Déterminer les valeurs efficaces des intensités des courants dans chaque dipôle. Chaque impédance est alimentée sous une tension composée U = 230 *3½ = 400 V J = 400/46 = 8,7 A. Déterminer les valeurs efficaces des intensités des courants dans les fils de phase. I = J3½ = 8/,7*1,732 = 15 A. Calculer la puissance électrique absorbée par l'ensemble de ces trois dipôles. P = U I 3½ cos j avec cos j = 1 ; I= 15 A (intensité en ligne) et U = V 3½ ( tension composée) P = 400*15*1,732= 10350 W. Un moteur est branché dans cette installation, en parallèle avec les dipôles résistifs ; il a les caractéristiques suivantes : Pa = 9 kW ; U= 400 V ; cos j = 0,80. Calculer les puissances actives et réactives absorbées par l'installation.  puissance active : P= 3½ U I cos j Puissance réactive : Q= 3½ U I sin j = P tan j Puissance apparente ( Pabsorbée) : S =3½ U I = P/cos j Puissance active(W) Q (var) S( VA) résistance 10350 0 10350 moteur 9000 cos j = 0,80 ; tan j = 0,75 Q= 9000*0,75=6750 11250=11250 total P=19350 Q=6750 Stotal =(P2+Q2)½=20500 Déterminer l'intensité efficace du courant en ligne alimentant l'installation. Stotal =3½ U Itotal soit Itotal = Stotal /(3½ U ) = 20500/(1,732*400) =29,6 A.

retour -menu