Dosage des ions chlorures : potentiométrie, conductimétrie capes agricole 2004

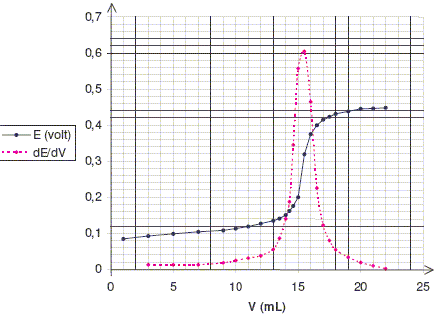
On veut vérifier la teneur en ions chlorure d’un sérum physiologique. Pour cela, on ajoute progressivement une solution de nitrate d’argent de concentration C = 0,100 mol.L^-1 à un volume V₀ = 50,0 mL d’une solution S préparée en diluant cinq fois le sérum étudié et on suit l’évolution correspondante de la différence de potentiel E entre une électrode d’argent et une électrode au calomel saturé (notée E.C.S.). Les résultats obtenus sont donnés ci-dessous :

 Donner l’expression du potentiel d’oxydoréduction de l’E.C.S.. Pourquoi est-il constant à température constante ?

L'électrode de référence utilisée ici est une électrode au calomel saturée (ECS), c'est à dire une électrode de platine (Pt) recouverte de mercure (Hg) sur lequel est déposé du calomel Hg₂Cl₂. Cette électrode est dite saturée car la solution dans laquelle plonge l'électrode ainsi constituée est une solution aqueuse saturée en chlorure de potassium KCl.

couple Hg₂Cl₂ (s)/ Hg (l) : Hg₂Cl₂ (s)+ 2e^- =2 Hg(l) + 2Cl^-.

E_réf = E°[ Hg₂Cl₂ (s)/ Hg (l)] + 0,03 log 1/[Cl^-]².

E_réf = 0,27 -0,06 log [Cl^-].

Dans la solution saturée en KCl : [Cl^-] = 4,7 mol/L à 25 °C.

E _réf = 0,27 -0,06 *log 4,7 = 0,23 V.

Quelle précaution faut-il prendre avec l’électrode au calomel lorsqu’on réalise un tel dosage ? Les ions argent, en contact au niveau du verre fritté (paroi poreuse à l’extrémité de l’électrode) avec les ions chlorure de l’ECS,donne un précipité de chlorure d’argent. Ce dernier bouche le verre fritté ; l'électrode devient inutilisable. On ajoute à l’E.C.S une allonge en verre remplie d’une solution de nitrate de potassium. La conduction électrique demeure ; il n'y a plus contact direct entre les ions chlorure de l'électrode et la solution contenant les ions Ag+.

Déterminer la concentration molaire volumique des ions chlorure dans la solution S puis dans le sérum.

Ag⁺(aq) + Cl^-(aq) = AgCl(s).

A l'équivalence les quantités de réactifs mis en présence sont en proportions stoechiométriques :

C V_éq = V₀ C_S avec V_éq = 15,5 mL ( lecture graphe) ; V₀ = 50,0 mL ; C= 0,100 mol/L.

C_S = 0,100*15,5/50,0 = 3,10 10^-2 mol/L.

C_sérum = 5 C_S =5* 3,10 10^-2 = 0,155 mol/L.

Comparer à l’indication portée sur l’étiquette du sérum : 0,9 % en masse de chlorure de sodium.

Masse molaire NaCl : M= 35,5+23 = 58,5 g/mol.

M*C_sérum =58,5*0,155 = 9,07 g/L

La densité du sérum est égale à 1 : 0,907 g de NaCl dans 100 g de sérum ou 0,91%.

Valeur en accord avec celle de l'étiquette.

Déterminer la valeur du produit de solubilité du chlorure d’argent en utilisant les valeurs de la différence de potentiel à V1 = 10,0 mL et à V2 = 20,0 mL. E1 = 0,115 V ; E2 = 0,445 V ( lecture graphe) ; DE= E2 -E1 =0,33 V. Ag+(aq) + Cl-(aq) = AgCl(s). Ks = [Ag+(aq)] [Cl-(aq)] d'où [Ag+(aq)] = Ks / [Cl-(aq)] Ag+(aq) + e- = Ag(s). E = E°(Ag+(aq) / Ag(s)) + 0,06 log [Ag+(aq)] E = E°(Ag+(aq) / Ag(s)) + 0,06 log Ks -0,06 log [Cl-(aq)] E= E°(AgCl(s)/Ag(s) -0,06 log [Cl-(aq)]. (1) E1 ( ou E2) = E-EECS= E-0,23.

V₁ = 10 mL ajouté : avant l'équivalence, l'ion chlorure est en excès de :

 C_SV₀-CV₁ = 0,031*50-0,1*10 = 0,55 mmol ; [Cl^-(aq)] = 0,55 / (V₀+V₁ ) = 0,55 / 60 = 9,16 10^-3 mol/L.

Repport dans (1) : 0,115 = E°(AgCl(s)/Ag(s)-E_ECS -0,06 log 9,16 10^-3 ;

E°(AgCl(s)/Ag(s)-E_ECS = 0,115+0,06 log 9,16 10^-3 = -7,3 10^-3.(2)

 C(V_éq-V₁ ) =0,1*(20-15,5) = 0,45 mmol ; [Ag⁺(aq)] = 0,45 / (V₀+V₂ ) = 0,45 / 70 = 6,43 10^-3 mol/L.

(1) et (2) donnent : 0,445 = -7,3 10^-3 -0,06 log [Cl^-(aq)] ;

log [Cl^-(aq)] = (-7,3 10^-3 -0,445)/ 0,06 = -7,54 ; [Cl^-(aq)] = 2,9 10^-8 mol/L

K_s = [Cl^-(aq)] [Ag⁺(aq)] = 2,9 10^-8* 6,43 10^-3 ; K_s =1,86 10^-10.

Déterminer la valeur du potentiel standard d’oxydoréduction du couple Ag⁺(aq) / Ag(s).

(2) donne : E°(Ag⁺(aq) / Ag(s)) + 0,06 log K_s -E_ECS = -7,3 10^-3.

E°(Ag⁺(aq) / Ag(s)) = -7,3 10^-3- 0,06 log 1,86 10^-10 +E_ECS= -7,3 10^-3 + 0,583 +0,23

E°(Ag⁺(aq) / Ag(s)) =0,80 V.

Le dosage précédent peut également être suivi par conductimétrie.

Faire un schéma clair d’une cellule de conductimétrie. Quelle est la grandeur qui est alors effectivement mesurée ?

La cellule conductimétrique est constituée de deux plaques rectangulaires de platine platinés, de surface S, parallèles à une distance l sur un support en verre. On mesure la résistance R ( ohm) du volume de liquide délimité par les plaques ; la cellule indique la conductance G = 1/R ( siemens ).

En quoi consiste l’étalonnage d’un conductimètre ?

Le fabricants fournit une table de la conductivité d’une solution de chlorure de potassium à 0,1 mol /L pour toutes les températures allant de 15,0 à 30,0°C.

On mesure alors la conductance de cette solution de chlorure de potassium et la température de la solution.

Les conductimétres sont munis d’un potentiométre d’étalonnage qui permet d’ajuster la valeur lue à la valeur donnée par la table du fabricant.

Est-il utile d’étalonner un conductimètre pour réaliser un dosage conductimétrique ?

Non : afin de déterminer le volume équivalent, on recherche l'intersection de deux droites.

Quelles sont les conditions nécessaires pour obtenir des portions de droites lors d’un dosage conductimétrique ?

Le volume de la solution du bécher doit être paratiquement constant : utiliser un grand volume de solution à titrer ( ajouter de l'eau distillée) et ajouter à la burette graduée, un petit volume de solution titrante ( donc beaucoup plus concentrée que la solution à titrer).

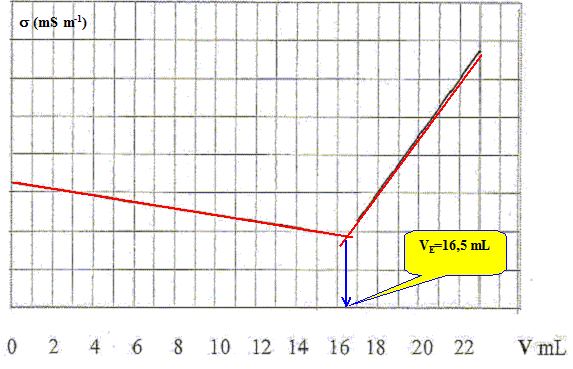
 Les conductivités molaires ioniques limites ( mS.m².mol^-1) de quelques ions sont indiquées ci-dessous :

l° _Na+ = 5,01 ; l° _Cl- = 7,63 ; l° _Ag+ = 6,19 ; l° _NO3-= 7,14.

Indiquer l’allure de la courbe donnant les variations du produit : «conductivité . Volumesolution»

Pour justifier le tracé ainsi réalisé, donner l’expression et la valeur des pentes des portions de droites obtenues.

Equation de la réaction associée à ce dosage : Ag⁺ _aq + Cl^- _aq ---> AgCl _solide.

Avant l'équivalence :

L'ion argent est en défaut ; l'ion chlorure est en excès ; les ions nitrate et sodium sont spectateurs. ( les ions oxonium et hydroxyde sont minoritaires)

s = l_Na+[Na⁺] + l_Cl-[Cl^-] + l_NO3-[NO₃^-]

On ajoute x = CV mol d'ion argent ( qui demeure en défaut ) et x = CV mol d'ion nitrate.

x mol d'ion chlorure disparaissent : du point de vue de la conductivité, tout se passe comme si on remplaçait l'ion chlorure par l'ion nitrate.

Or l_Cl- > l_NO3- donc la conductivité de la solution diminue.

On note V₀ le volume de la solution dans le becher et V le volume de nitrate d'argent ajouté à la burette.

On note C la concentration du nitrate d'argent et C_S celle du chlorure de sodium.

[Na⁺] =V₀ C_S / (V₀+V) ; [Cl^-] =(V₀ C_S -C V)/ (V₀+V) ; [NO₃^-] =CV/ (V₀+V)

s = [l_Na+V₀ C_S + l_Cl-(V₀ C_S -C V)+ l_NO3-CV]/ (V₀+V)

s = [(l_Na+ + l_Cl-) V₀ C_S + ( l_NO3- -l_Cl-)CV]/ (V₀+V)

s (V₀+V) = (l_Na+ + l_Cl-) V₀ C_S + ( l_NO3- -l_Cl-)CV

On trace s (V₀+V) = f(V) : droite de pente : ( l_NO3- -l_Cl-)C = (7,14-7,63)*0,1 = -0,049 S m^-1.

L'ion chlorure est en défaut ; l'ion argent est en excès ; les ions nitrate et sodium sont spectateurs. ( les ions oxonium et hydroxyde sont minoritaires)

s = l_Na+[Na⁺] + l_Ag+[Ag⁺] + l_NO3-[NO₃^-]

on ajoute x = CV mol d'ion argent ( qui est en excès de C(V-V_E) ) et x = CV mol d'ion nitrate.

L'ajout d'ions en solution se traduit par une augmentation de la conductivité de la solution.

[Na⁺] =V₀ C_S / (V₀+V) ; [Ag⁺] =C(V-V_E)/ (V₀+V) ; [NO₃^-] =CV/ (V₀+V)

s = [l_Na+V₀ C_S + l_Ag+C(V-V_E)+ l_NO3-CV]/ (V₀+V)

s = [l_Na+V₀ C_S - l_Ag+C V_E + ( l_NO3- +l_Ag+)CV]/ (V₀+V) ; or V₀ C_S = C V_E

s (V₀+V) = (l_Na+ - l_Ag+ ) V_E C + ( l_NO3- +l_Ag+)CV

On trace s (V₀+V) = f(V) : droite de pente :( l_NO3- +l_Ag+)C = (7,14+6,19)*0,1 = +1,33 S m^-1.