Circuit à looping; théorème de l'énergie cinétique; base de Frenet capesa 2004

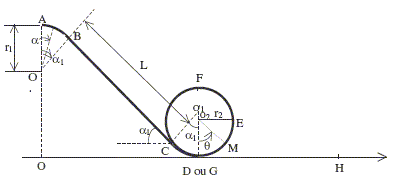
Le rail est constitué de plusieurs parties : une portion de cercle AB (rayon r₁, angle a₁) une partie rectiligne BC de longueur L puis une portion de cercle CD de rayon r₁ suivie d'un tour d'hélice : DEFG, de rayon r₂ et d'axe horizontal (voir schéma), prolongée par une portion rectiligne horizontale GH.

On considère pour la résolution de l'exercice que la portion de circuit constituée par un tour d'hélice et le segment rectiligne GH sont contenus dans le plan vertical de la section initiale. La droite BC est tangente en B à la portion de cercle AB et est de même tangente en C à la portion de cercle CD.

Le chariot est lâché sans vitesse initiale du point A. On note g l’intensité du champ de pesanteur terrestre.

Le référentiel terrestre est considéré comme galiléen.

Données : g = 9,81 m.s^-2 ; m = 1000 kg ; r₁ = 2,5 m ; r₂ = 2,0 m.

Donner l'expression littérale de la vitesse du chariot en B en C puis en D en fonction de r₁, L, a₁ et g.

Le chariot est soumis à son poids et à l'action du support.

L'action du support est constamment perpendiculaire à la vitesse ( absence de frottement) et, en conséquence, elle ne travaille pas.

Parcours AB : le travail du poids est moteur en descente

La différence d'altitude entre A et B vaut h₁ = r₁(1-cos a₁ ) ; travail du poids : W₁= mgh₁ = mg r₁(1-cos a₁ )

variation de l'énergie cinétique : DEc = ½mv²_B-0 = ½mv²_B.

théorème de l'énergie cinétique : ½mv²_B = mg r₁(1-cos a₁ ) ; v²_B = 2g r₁(1-cos a₁ ).

v_B = [2g r₁(1-cos a₁ )]^½.

Parcours BC : le travail du poids est moteur en descente La différence d'altitude entre C et B vaut h2 = Lsin a1; travail du poids : W2= mgh2 = mg Lsin a1. variation de l'énergie cinétique : DEc = ½mv2C-½mv2B. théorème de l'énergie cinétique : ½mv2C -½mv2B = mg Lsin a1. v2C =v2B +2g Lsin a1. vC = [v2B +2g Lsin a1]½.

Parcours CD : le travail du poids est moteur en descente

La différence d'altitude entre C et D vaut h₃ = r₁(1-cos a₁ ) ; travail du poids : W₃= mgh₃ = mg r₁(1-cos a₁ )

variation de l'énergie cinétique : DEc = ½mv²_D-½mv²_C.

théorème de l'énergie cinétique : ½mv²_D -½mv²_C = mg r₁(1-cos a₁ ) ; v²_D = v²_C +2g r₁(1-cos a₁ ).

v_D = [ v²_C +2g r₁(1-cos a₁ )]^½.

Déterminer la vitesse du chariot à son passage en M sur l'hélice (assimilée à un cercle) repéré par l’angle q.   Parcours DM : le travail du poids est résistant en montée. La différence d'altitude entre M et D vaut h4 = r2(1-cos q ) ; travail du poids : W4= -mgh43 = -mg r2(1-cos q ) variation de l'énergie cinétique : DEc = ½mv2M-½mv2D. théorème de l'énergie cinétique : ½mv2M -½mv2D = -mg r2(1-cos q ) ; v2M = v2D -2g r2(1-cos q ). vM = [ v2D -2g r2(1-cos q )]½.

En déduire la condition sur L pour que le chariot arrive en E (q_E =90°).

On atteint E si la vitesse en ce point est positive ou nulle.

Or v²_E = v²_D -2g r₂(1-cos 90 ) = v²_D -2g r₂.

d'où : v²_D >=2g r₂.

Or v²_D = v²_C +2g r₁(1-cos a₁ ) et v²_C =v²_B +2g Lsin a₁ et v²_B = 2g r₁(1-cos a₁ )

v²_D = 2g r₁(1-cos a₁ ) +2g Lsin a₁ +2g r₁(1-cos a₁ )

v²_D = 2g( r₁+ r₁)(1-cos a₁ ) +2g Lsin a₁.

d'où : 4g r₁(1-cos a₁ ) +2g Lsin a₁>=2g r₂.

2g Lsin a₁>=2g r₂-4g r₁(1-cos a₁ )

L >=[ r₂-2 r₁(1-cos a₁ )] / sin a₁.

L₁=[ r₂-2 r₁(1-cos a₁ )] / sin a₁.

L₁ = [2-5*(1-cos50)/sin50 ; L₁ = 0,28 m.

En déduire son expression en B. Calculer sa valeur numérique. Conclure.

v²_B/r₁= 2g (1-cos a₁ ) ; R_B= m[g cos a₁-2g (1-cos a₁ )] ; R_B= mg [3 cos a₁-2].

R_B= 1000*(3 cos50-2) = -72 N

Le solide a décollé ( quitté la piste) avant d'atteindre B.

Déterminer la valeur de a quand le chariot quitte la piste entre A et B.

R_B=0 = mg [3 cos a-2] soit cos a = 2/3 ; a = 48°. 

À partir de cette question on va choisir une nouvelle valeur a₁ = 45°, afin que le chariot ne quitte pas la piste entre A et B.

Établir l'expression de la réaction du rail sur sa partie rectiligne BC. Calculer sa valeur.

R= mg cos a₁ = 1000*9,81*cos45 =6,9 10⁴ N.

Établir l'expression de la réaction du rail sur la partie circulaire (de rayon r₂) en fonction de q, m, g, r₁, r₂, a₁ et L (le chariot circule à l'intérieur du cercle).

v²_M = v²_D -2g r₂(1-cos q ) ; Or v²_D = v²_C +2g r₁(1-cos a₁ ) et v²_C =v²_B +2g Lsin a₁ et v²_B = 2g r₁(1-cos a₁ ).

v²_M = 2g r₁(1-cos a₁ ) +2g Lsin a₁ +2g r₁(1-cos a₁ ) -2g r₂(1-cos q ).

v²_M = 4g r₁ (1-cos a₁ ) +2g Lsin a₁ -2g r₂(1-cos q ).

v²_M /r₂= 4g r₁ /r₂ (1-cos a₁ ) +2g/r₂ Lsin a₁ -2g(1-cos q ).

R = mg[3 cosq-2 +2[ 2r₁ /r₂(1-cos a₁ ) + L/r₂sin a₁ ]].

Déterminer la condition sur L pour que le chariot puisse parcourir la boucle.

La réaction du support doit être positive ou nulle lorsque q= p.

3 cosp-2 +2[ 2r₁ /r₂(1-cos a₁ ) + L/r₂sin a₁ ]>=0.

2r₁ /r₂ (1-cos a₁ ) + L/r₂sin a₁ >= 2,5.

L/r₂sin a₁ >= 2,5- 2r₁ /r₂ (1-cos a₁ )

L>= [2,5- 2r₁ /r₂(1-cos a₁ )]r₂ / sin a₁.

En déduire l'expression de la valeur minimale de L notée L₂. Calculer sa valeur numérique.

L₂= [2,5- 2r₁ /r₂ (1-cos a₁ )]r₂ / sin a₁.

L₂=[2,5-2,5(1-cos45)]*2/sin45 =5,0 m.

Par raison de sécurité, on veut que la réaction du rail soit toujours supérieure au quart du poids du chariot.

Déterminer la nouvelle valeur minimale L₃, permettant au chariot d’arriver en G en toute sécurité, après un tour. Calculer sa valeur numérique.

3 cosp-2 +2[ 2r₁ /r₂ (1-cos a₁ ) + L₃/r₂sin a₁ ]=0,25

2r₁ /r₂ (1-cos a₁ ) + L₃/r₂sin a₁=2,625

L₃/r₂sin a₁=2,625 -2r₁ /r₂(1-cos a₁ )

L₃=[2,625 -2r₁ /r₂(1-cos a₁ )]r₂ /sin a₁.

L₃=[2,625-2,5(1-cos45)]*2/sin45 =5,35 m.

Calculer v_G après ce tour.

v_D =v_G= [ v²_C +2g r₁(1-cos a₁ )]^½ ; v²_C =v²_B +2g Lsin a₁ et v²_B = 2g r₁(1-cos a₁ ).

v_G= [ 2g r₁(1-cos a₁ ) +2g L₃sin a₁ +2g r₁(1-cos a₁ )]^½ ;

v_G= [ 2g[2r₁(1-cos a₁ ) + L₃sin a₁]]^½.

v_G=[ 2*9,81[5*(1-cos 45) + 5,9*sin45]]^½ ; v_G= 10,4 m/s.

Il aborde alors la dernière partie rectiligne (GH) de la piste sur laquelle il subit une force de freinage de valeur f=mg/4.

Calculer la longueur minimale DS = OH de ce circuit à looping pour rester dans des conditions de sécurité.

Sur cette partie horizontale seule la force de freinage travaille, le poids et l'action du plan étant perpendiculaires à la vitesse.

Travail résistant des forces de freinage : W = -f DS = -mg DS/4.

Théorème de l'énergie cinétique : 0-½mv²_G= -mg DS/4.

v²_G=g DS/2 ; DS= 2v²_G/g =2*10,4²/9,81 ; DS= 22 m.