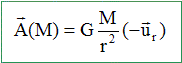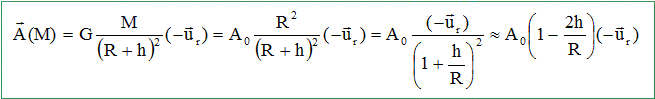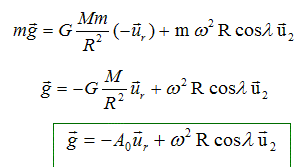Champ gravitationnel de la terre ; champ de pesanteur terrestre concours Capes interne 2008

Les vecteurs sont écrits en gras et en bleu. La tere est assimilée à une sphère homogène de centre O, de masse M et de rayon R.  On note r=OM la distance du centre de la terre au point M et ur = OM/r. On note G, la constante de gravitation et A(M) le champ gravitationnel créé par la terre en M. G=6,67 10-11 Nm2kg-2 ; M= 6 1024 kg ; R= 6380 km. Soit r la masse volumique de la terre. Le fait d'assimiler la terre à une sphère homogène revient à faire quelle hypothèse sur r ? La masse volumique de la terre est constante. On note r0 cette constante. Exprimer r0 en fonction de M et R. Calculer r0. volume d'une sphère : 4/3 p R3 ; r0 =3M/(4 p R3) avec R= 6,38 106 m. r0 = 3*6 1024 /(4*3,14*(6,38 106)3) ; r0 =5,52 103 kg m-3 proche de 6 103 kg m-3. Exprimer le champ gravitationnel créé par la terre en un point M extérieur à la terre, situé à la distance r. Quelle est la topographie des lignes de champ ? Par raison de symétrie, les lignes de champ sont radiales. Exprimer puis calculer le champ gravitationnel créé par la terre à sa surface. valeur de ce champ : A0 = GM/R2. A0 = 6,67 10-11*6 1024/(6,38 106)2 =9,83 m/s2 proche de 1 101 m/s2. Exprimer le champ gravitationnel à une altitude h au dessus de la surface de la terre. Que devient cette expression si h<<R ? On pose DA=A(h)-A0. Calculer |DA/A0| pour h = 10 km. A(h)-A0 = -A0 (2h/R) ; |DA/A0| = 2h/R. |DA/A0| = 2*10/6380 = 3,1 10-3 = 0,31 %. La variation est très faible. Ce champ peut être considéré comme constant tant que h est inférieur à 10 km. C'est le cas des tirs balistiques ou des lâchés de ballon en météorologie. On suppose que le référentiel terrestre est galiléen. Comment définit-on un référentiel ? Un référentiel est un objet par rapport auquel on étudie le mouvement d'un corps. Comment définit-on un référentiel galiléen ? Dans un référentiel galiléen, les lois de newton s'appliquent. Rappeler la loi fondamentale de la statique des fluides dans un référentiel galiléen. pA-pB = rg(hA-hB). pression en Pa ; masse volumique r en kg m-3 ; g en m/s2 ; h : altitude en m. Quelle est l'allure de la surface libre des océans ? La terre est considérée comme une sphère homogène. En l'absence de vent, la surface des océans est à la même distance du centre de la terre. En négligeant la rotation de la terre, la surface de l'eau est plane.  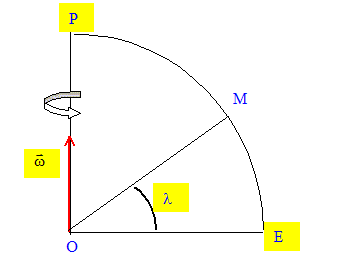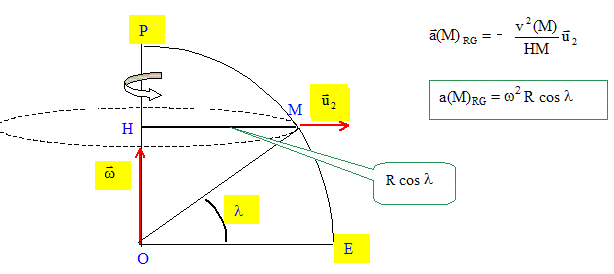Influence de la rotation de la terre. La tere est animée d'un mouvement de rotation uniforme autour de l'axe des pôles, à la vitesse angulaire w=7,29 10-5 rad/s. Soit M un point de la surface situé à la latitude l. Faire un schéma indiquant sur un quart de circonférence, le pôle nord P, l'équateur E, le point M, la latitude l, le vecteur vitesse angulaire w. 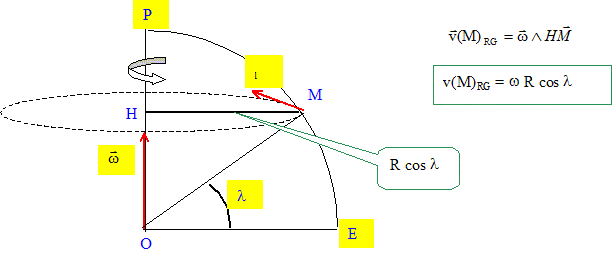Le référentiel géocentrique RG est supposé galiléen. Comment définit-on ce référentiel ? Le référentiel héliocentrique a pour origine le Soleil et des axes pointant vers des étoiles lointaines qui paraissent fixes. Le référentiel géocentrique a pour origine le centre de la Terre et des axes parallèles à ceux du référentiel héliocentrique. Exprimer, dans le référentiel géocentrique, la vitesse du point M, notée v(M)RG, en fonction de R, w, l et d'un vecteur u1 que l'on représentera sur le schéma. Déterminer puis calculer la valeur de cette vitesse en P et en E. Au point P, cette vitesse est nulle ; au point E, cos l =1 et v(E)= w R. v(E) = 7,29 10-5 *6,38 106 = 465 m/s. Exprimer, dans le référentiel géocentrique, l'acélération du point M, notée a(M)RG, en fonction de R, w, l et d'un vecteur u2 que l'on représentera sur le schéma. 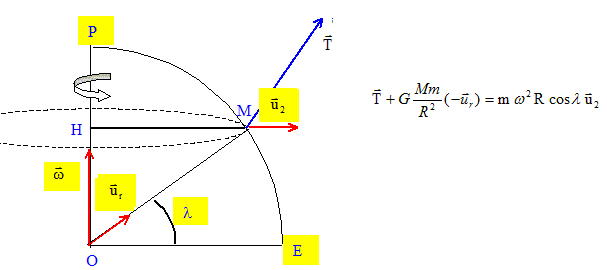Déterminer puis calculer la valeur de cette accélération en P et en E. Au point P, cette accélération est nulle ; au point E, cos l =1 et a(E)= w2 R. a(E) = (7,29 10-5 )2*6,38 106 = 3,39 10-2 m/s2. M assimilé à un point matériel de masse m, est fixé à un fil à plomb immobile à la surface de la terre. Appliquer la relation fondamentale de la dynamique à M(m) dans le référentiel géocentrique. On suppose que M(m) n'est soumis qu'à la force gravitationnelle exercée par la terre au point M et à la tension T du fil. Dans le référentiel terrestre, le poids de M(m) est défini comme l'opposé de la tension définie précédemment. Déterminer l'expression du champ de pesanteur g(M) dans le référentiel terrestre. Soit g(P) et g(E) la valeur du champ de pesanteur en P et en E. Déterminer puis calculer g(P) et g(E). valeur de g(P) = A0 = 9,83 m/s2. valeur de g(E) = A0-w2R = 9,83-3,39 10-2 =9,796 = 9,80 m/s2. La valeur de g(M) est différente au pôle et à l'équateur : la surface libre des océans ne sera pas plane. Influence de l'aplatissement de la terre aux niveaux des pôles.  La terre est aplatie aux niveaux des pôles, ce qui modifie l'intensité de la pesanteur. RP =6357 km ; RE=6378 km. Les résultats expérimentaux conduisent à : g(P) = 9,82 m/s2 et g(E) 9,78 m/s2. Les écarts sont dus pour 2/3 à la rotation et pour 1/3 à son applatissement. En 1672, J.Richer constate qu'une horloge parfaitement réglée à Paris, retarde de 2 min par jour à Cayenne. On modélise le balancier d'une horloge par un pendule simple de longueur L. Rapeller l'expression de la période T d'un pendule simple. T= 2p [L/g]½. On suppose que le champ de pesanteur à Paris est gP=9,810 m/s2 et que le champ de pesanteur à Cayenne est gC= 9,780 m/s2. La longueur du pendule est L=1,000 m. L'horloge est parfaitement réglée à Paris. Quel est le retard de cette horloge, par jour, si elle est transportée à Cayenne ? période à Paris : 2 p [9,810]-½ = 2,0060667 s. période à Cayenne : 2 p [9,780]-½ = 2,009141 s. Retard : 3,0744 10-3 s. retard par jour : 24*1800*3,0744 10-3 =132,8 s = 2 min 13 s.

retour -menu