Influence du pH sur la stabilité du diiode en solution aqueuse concours Capes interne 2008

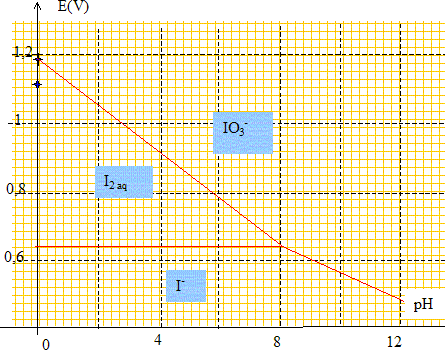
Déterminer le nombre d'oxydation de l'iode dans l'ion iodate IO3-. n.o(I) +3 n.o(O) = -1 avec n.o(O) - -2 d'où n.o(I) = +V. Soient les deux couples redox IO3- aq/I2aq et I2aq/I-aq. Ecrire les demi-équations électroniques pour ces deux couples. 2IO3- aq+ 12H+aq + 10e- = I2aq+ 6H2O. I2aq+2e- =2I-aq. Expliciter les potentiels d'électrode correspondants : E1 = E°(IO3- aq/I2aq ) + 0,06/10 log([IO3- ]2[H+]12/ [ I2]) E2 = E°( I2aq/I-aq ) + 0,03 log([ I2]/ [I-]2) Le potentiel de Nernst dépend de la température. Justifier. Le potentiel de Nernst découle des potentiels chimiques : ces derniers dépendent de la température. Pour chacun de ces couples, calculer le potentiel de Nernst à pH=0 et à pH=10 à la frontière de prédominance des deux espèces. On prendra les concentrations des espèces considérées égales à 0,100 mol/L sur cette frontière. E°(IO3- aq/I2aq ) = 1,19 V ; E°( I2aq/I-aq ) = 0,62 V. E1 = 1,19 + 6 10-3 log([0,1]2[H+]12/ [ 0,1]) = 1,19 + 6 10-3 log 0,1 + 6 10-3 *12 log [H+] E1 = 1,19 - 6 10-3 +0,072 log [H+] ; E1 = 1,18 - 0,072 pH. à pH 0 : E1 = 1,18 V ; à pH=10 : E1 = 0,464 V ;  E2 = 0,62 + 0,03 log([ 0,1]/ [0,1]2) = 0,62 +0,03 log 10 ; E2 =0,65 V. Tracer les diagrammes de prédominance des espèces relatives à ces couples et conclure quand à la stabilité du diiode à ces pH. IO3- aq+ 6H+aq + 6e- = I- aq+ 3H2O. E3 =E°(IO3- aq/ I- aq) + 0,01 log([IO3- ][H+]6/ [ I- ]) E3 =E°(IO3- aq/ I- aq) + 0,01 log ([IO3- ]/ [ I- ]) -0,06 pH A pH =0 le diiode est stable en solution ; à pH=10 le diiode s'est dismuté en ion iodure et en ion iodate. On dispose d'un volume V=100,0 mL d'une solution de pH=10 contenant n1 = 1,00 10-4 mole d'iodate de sodium (Na+ ; IO3-) et n2 = 2,00 10-2 mol d'iodure de potassium (K+ ; I-). Ces deux solides sont totalement solubles dans l'eau. Que se passe t-il si on acidifie, sans variation de volume, la solution jusqu'à pH=0 ? Médiamutation : obtention d'un degré d'oxydation intermédiaire à partir de composés de degrés d'oxydation différents. 2IO3- aq+ 12H+aq + 10e- = I2aq+ 6H2O.(2) 10I-aq= 5I2aq+10e-. (3) (2) + (3) donne : IO3- + 5I- + 6 H+= 3I2 + 3H2O. (4) Calculer la constante d'équilibre correspondante. K = [I2]3 /([IO3-][I-]5[H+]6). E1 = E°(IO3- aq/I2aq ) + 0,06/10 log([IO3- ]2[H+]12/ [ I2]) E2 = E°( I2aq/I-aq ) + 0,03 log([ I2]/ [I-]2) A l'équilibre E1 =E2 : E°(IO3- aq/I2aq ) + 0,06/10 log([IO3- ]2[H+]12/ [ I2]) = E°( I2aq/I-aq ) + 0,03 log([ I2]/ [I-]2) E°(IO3- aq/I2aq ) - E°( I2aq/I-aq ) = 0,03 log([ I2]/ [I-]2) -0,006 log([IO3- ]2[H+]12/ [ I2]) E°(IO3- aq/I2aq ) - E°( I2aq/I-aq ) =0,006 log ([ I2]6/ ([IO3- ]2[H+]12[I-]10)) E°(IO3- aq/I2aq ) - E°( I2aq/I-aq ) =0,012 log K log K = (1,19-0,62) / 0,012 ; log K= 47,5 ; K = 3,2 1047. Valeur très grande, la réaction est quantitative. Quelle concentration maximale en diiode peut-on obtenir ? "n1 = 1,00 10-4 mole d'iodate de sodium (Na+ ; IO3-) et n2 = 2,00 10-2 mol d'iodure" L'ion iodate est en défaut ( réactif limitant) . D'après les nombres stoechiométriques de (4) : n(I2 )= 3 n(IO3-) = 3n1 = 3,00 10-4 mole de diiode dans V= 0,100 L [I2]max = 3,00 10-3 mol/L. Quel doit être le pH de la solution pour obtenir 90% de cette concentration maximale en diiode ? [I2] =0,9 [I2]max = 2,70 10-3 mol/L soit xf = [I2] *V =2,70 10-4 mol avancement (mol) IO3- + 5I- + 6 H+ = 3I2 + 3H2O initial 0 n1 n2 0 solvant en large excès en cours x n1-x/3 n2-5/3x x fin xf =2,70 10-4 n1-xf /3 =10-5 n2-5/3xf = 1,955 10-2 xf [I-] = 1,955 10-2 / 0,1 = 0,1955 mol/L ; [IO3-] =10-5/0,1 =10-4 mol/L L'expression de K donne : [H+]6 = [I2]3/(K [IO3-][I-]5. [H+]6=( 2,70 10-3)3/[1047,5*10-4*0,19555]= 0,697 10-48. [H+] = 0,94 10-8 ; pH= 8,0.

retour -menu