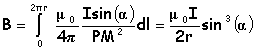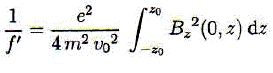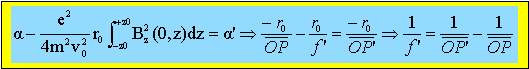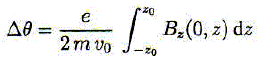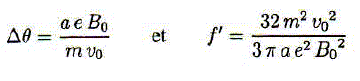Lentille magnétique; Concours Capes externe 2008

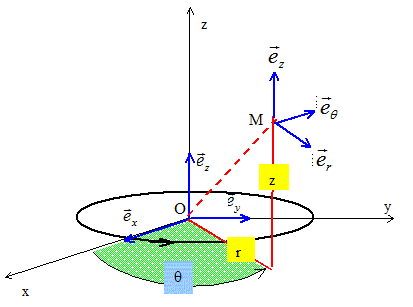
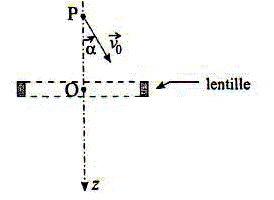
Le contrôle de la focalisation du faisceau électronique dans le microscope électronique est possible en utilisant des lentilles magnétiques. La lentille magnétique est modélisée par une bobine à N tours confondus, circulaires de rayon a, de centre O, d'axe Oz et parcourue par un courant permanent d'intensité I. Un point M de l'espace sera repéré par ces coordonnées cylindriques (r, q, z) et d'axe Oz et de centre O. Les vecteurs sont écrits en gras et en bleu. Préciser sur un schéma les coordonnées cylindriques du point M, ainsi que la base locale cylindrique ( er, eq, ez). 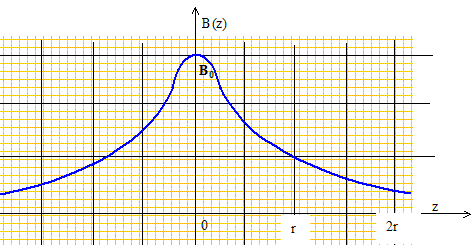Expression du champ magnétique B(M) crée par la spire. L'axe Oz est axe de symétrie du système ; une rotation autour de cet axe ne modifie pas le champ : la variable q n'intervient donc pas dans l'expression du champ. Tout plan contenant l'axe Oz est plan d'antisymétrie : le champ appartient donc au plan contenant l'axe Oz et le point M d'où : Bq( r, z) =0. Expression du champ magnétique en coordonnées cylindriques : B(M) = Br( r, z) er + Bz( r, z) ez. En pratique le faisceau électronique passe dans le domaine r<< a. Dans ce cas on peut se contenter d'une expression approchée du champ B au voisinage de l'axz Oz. B(M) ~ -½r dBz(0,z)/dz er +Bz( O, z) ez. On sait que pour la spire circulaire, Bz( O, z) = B0[1+z2/a2]-1,5 avec B0 = m0 NI/(2a). Donner la méthode d'obtention de ce résultat et préciser sur une figure adéquate l'orientation du courant I correspondant.   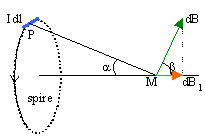l'élément de courant Idl crée en M , le champ élémentaire dB, perpendiculaire à PM, de module : Idl et PM étant perpendiculaire sin(q)=1 Par raison de symétrie le champ résultant sera porté par l'axe horizontal. La composante utile sera dBcos(b) = dBsin(a) Pour tous les éléments Idl, l'angle a et PM sont les mêmes. L'intégration de dB sur toute la spire donne le module du champ résultant ( sin a = rayon r / PM ) Au centre de la spire a=90°et sin a =1 d'où B0 =m0I/(2r). cotan a = z/r ; 1+cotan2a= 1/sin2a ; sina = 1/(1+cotan2a)½ =[1+(z/r)2]-½ par suite B=B0[1+(z/r)2]-3/2     Tracer le graphe représentatif de f(z) = Bz(O,z).  Que vaut f(10a) ? Comment éaliser expérimentalement le tracé de cette courbe ? f(10a) = Bz( O, 10a) = B0[1+100]-1,5 = 10-3 B0. Les relevés expérimentaux se font à l'aide d'une sonde de Hall longitudinale que l'on déplace sur l'axe de la bobine.    On place en un point P de l'axe Oz, en amont de la lentille magnétique, une source ponctuelle d'électrons. On considère un électron émis depuis le point P avec une vitesse v0. On ajoute les hypothèses simplificatrices suivantes : - l'électron est supposé non relativiste. - L'électron ne suit que le force magnétique due à la lentille. - Le vecteur vitesse initiale v0 est dans le plan méridien q=0 et forme un angle a avec Oz. L'angle a est faible et la trajectoire ultérieure de l'électron reste dans le domaine r<< a.   A quelle approximation d'optique une hypothèse simplificatrice fait-elle penser ? La dernière hypothèse est comparable aux conditions de Gauss en optique. Le référentiel du laboratoire où la lentille magnétique est fixe, est galiléen. Définir les termes référentiel et référentiel galiléen. référentiel : objet par rapport auquel on se repère pour l'étude du mouvement d'un système ; on lui associe un repère et une origine des temps. référentiel galiléen : dans ce référentiel le principe d'inertie ou 1ère loi de Newton s'applique " un point matériel pseudo-isolé demeure dans son état de repos ou de mouvement rectiligne uniforme". Donner l'expression de la force magnétique subie par l'électron à un instant quelconque en fonction de e, du champ magnétique B(M) au point M où il se trouve et de la vitesse v. Force de Lorentz : Déterminer l'ordre de grandeur de la valeur du champ magnétique à partir de laquelle on peut ne pas tenir compte du poids de l'électron dans l'étude du mouvement. On suppose que la vitesse de l'électron est de l'ordre de 108 m/s. mg~ 9,1 10-31*10 = 9 10-30 N ; F= evB = 1,6 10-19*108B = 1,6 10-11 B. La valeur de la force de Lorentz est égale à la valeur du poids si B = 6 10-19 T. Or la valeur expérimentale de B est toujours supérieure à 10-3 T, donc le poids est toujours négligeable devant la force de Lorentz.     Enoncer la relation fondamentale de la dynamique pour un point matériel. La somme vectorielle des forces extérieures appliquées au système est égale au produit de la masse du système par le vecteur accélération de son centre d'inertie. Exprimer l'accélération de l'électron au point M par rapport au référentiel du laboratoire en coordonnées cylindriques (r, q, z) dans la base locale cylindrique ( er, eq, ez). 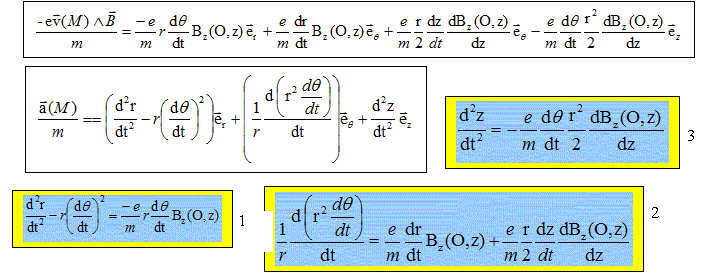Exprimer la relation fondamentale de la dynamique et en déduire les trois équations différentielles du mouvement de l'électron. 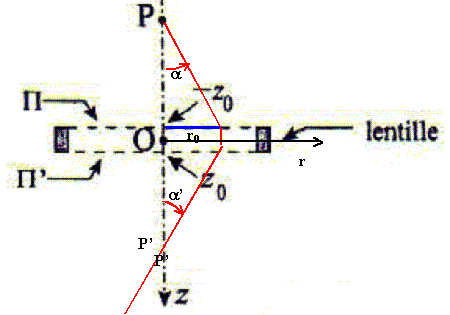Démontrer la relation suivante : dq/dt =e/(2m) Bz(O,z). Intégrer 2 par rapport au temps et tenir compte de " le vecteur vitesse initiale v0 est dans le plan méridien q=0 et forme un angle a avec Oz" L'équation 3 présente un second membre négigeable dans le cadre de cette étude ( car d'ordre 2 en r/a). Que vaut alors dz/dt ? dz/dt = Cte = v0 cos a ; or pour les petits angles cos a ~ 1 d'où dz/dt =v0. Déduire de 1, l'équation différentielle que vérifie l'évolution radiale de l'électron. d2r/dt2 - r e2/(2m)2Bz2(O,z) = -½e2/m2 r Bz2(O,z) d2r/dt2 +0,25 r e2/m2Bz2(O,z) =0. puis d2r/dt2 = d2r/dz2 *dz2 /dt2 =d2r/dz2 *v02. enfin : v02 d2r/dz2 +0,25 r e2/m2Bz2(O,z) =0. (4) On propose sur les figures ci-dessous deux familles de tracés de fonctions r(z) partant d'un point d'annulation avec un angle de départ a variable. Quelle figure représente effectivement un champ de solution possible de l'équation 4 ? Le système joue t-il le rôle attendu ? La dérivée seconde d2r/dz2 est toujours négative ; en conséquence la courbure de la fonction r(z) ne change pas : cas de la figure 12. Les électrons issus d'un point convergent en un point unique après avoir traversés la lentille magnétique : cette lentille est stigmatique et remplit son rôle. 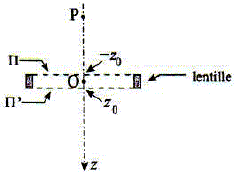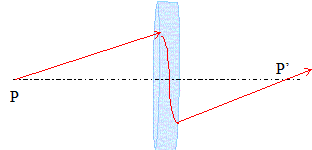On ajoute maintenant l'hypothèse lentille mince, c'est à dire que le champ magnétique de la bobine n'intervient que sur une faible épaisseur comprise entre deux plans P et P ', de positions -z0 et +z0 avec z0<<OP. On peut toujours écrire que : dq/dt =e/(2m) Bz(O,z). L'équation différentielle sur le mouvement radial r(z) est utilisable sous la forme approchée : d2r/dz2 ~ - e2/(2mv0 )2 r0 Bz2(O,z) où r0 est une valeur approchée de r(z) ( ordre zéro en r/a) entre deux plans P et P '. Pourquoi la trajectoire d'un électron seul est forcément rectiligne en dehors de la zone de champ magnétique. En dehors de la zone de champ magnétique, l'électron n'est soumis à aucune force : d'après le principe d'inertie le mouvement est rectiligne uniforme. Montrer que l'angle d'incidence a de l'électron en entrée de la zone magnétique est a ~(dr/dz)-z0~ -r0/OP. tan a = -r0/OP. Pour les petits angles -a ~ r0/OP ; de plus : a ~(dr/dz)-z0 d'où : a ~(dr/dz)-z0~ -r0/OP avec OP mesure algébbrique de OP. On note P' le point de focalisation du rayon électronique issu de la lentille, sur l'axe Oz et on pose a' l'angle d'émergence de la zone magnétique tel que : a' ~(dr/dz)+z0~ -r0/OP' avec OP' mesure algébbrique de OP'. Montrer que le système vérifie une loi de conjugaison de Descartes de lentille mince de centre O et de focale f' avec : Intégrer d2r/dz2 entre -z0 et +z0 : Pendant le passage de l'électron dans la zone de champ magnétique, l'électron ne reste pas dans un même plan méridien ; il y a un angle de rotation Dq autour de l'axe Oz de la trajectoire de l'électron qui vaut : résultat obtenu en intégrant dq/dt =dq/dz . dz/dt =dq/dz .v0= e/(2m) Bz(O,z) entre -z0 et +z0. Dans le cas de la spire,les intégrales pouvant être étendues e=de -oo à + oo, un calcul non demandé donne : Quel est le signe de f' ? Conséquence. f' étant positif, la lentille magnétique est convergente. Sur quels paramètres peut-on jouer pour réduire f' à tension accélératrice U fixée ? U étant fixée, la vitesse v0 est fixée. Diminuer f' c'est augmenter le produit aB02. B0 étant proprotionnel à N et à l'intensité I, il faut augmenter le nombre de spires de la bobine N ou l'intensité du courant. On donne B0 = 1T, a= 1 mm et on choisit U de telle manière que v0 = 2 108 m/s. Calculer f'. f' = 32*(9,1 10-31)2* 4 1016 / (3*3,14*10-3*(1,6 10-19)2) =4,4 10-3 m. Valeur assez faible, par rapport aux distances focales en optique : la lentille est très convergente. Calculer Dq et tracer dans l'espace l'allure de la trajectoire de l'électron de P en P'. Dq = 10-3*1,6 10-19 / (9,1 10-31*2 108) = 0,88 rad ( 50°). L'aberration "de charge d'espace" existe dans ce cas. Quelle en est l'origine ? Pourquoi la réduction de l'aberration passe par l'emploi de faisceaux électroniques peu denses ? L'électron étudié se trouve également dans un champ électrique crée par les autres électrons du faisceau, champ d'autant plus faible que le faisceau est peu dense. Avec un faisceau peu dense on peut négliger la force électrique due à ce champ devant la force de Lorentz.

retour -menu