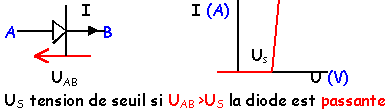Générateur de rampes Capes 2008

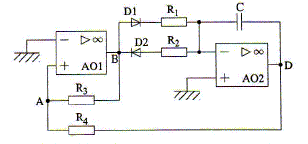
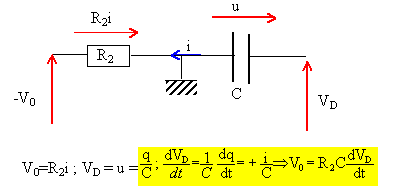
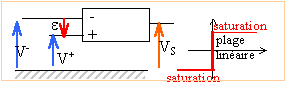
Les seules sources sont les alimentations continues +V0 = 15 V et -V0 = -15 V. La notation VM désigne le potentiel du point M. Chaque diode et chaque AO est supposé idéal. Tracer la caractéristique i=f(U) d'une diode idéale en convention récepteur. Si la diode est idéale la tension de seuil est nulle.  Tracer la caractéristique Vs=f(e) d'un AO idéal ( e = V+-V- ) et préciser les régime de fonctionnement. Fonctionnement linéaire : e =0 ; si e >0, alorsVs = +V0, saturation ; si e <0, alorsVs = -V0, saturation. Que peut-on dire des courants arrivant aux entrées inverseuse et non inverseuse d'un AO idéal ? L'impédance d'entrée étant infinie, les courants d'entrée sont nuls.     Qu'appelle t-on diviseur de tension. Enoncer et démontrer la formule du diviseur de tension. Montage électronique simple permettant d'obtenir une tension proportionnelle à une autre tension. On note i l'intensité traversant les deux impédances e = (Z1+Z2) i et s = Z2 i. s/ e = Z2 / (Z1+Z2) s = eZ2 / (Z1+Z2). Montrer que le potentiel VA vérifie : VA = (R3 VD+R4 VB) / (R3+R4 ). Théorème de Milleman appliqué en A : VA = [ VB/R3 + VD/R4 ) ] / (1/R3+1/R4 ). Réduire au même dénominateur R3R4 : VA = (R3 VD+R4 VB) / (R3+R4 ). Justifier que l'AO1 fonctionne en régime saturé et que l'AO2 fonctionne en régime linéaire. AO2 : présence d'une boucle de contre réaction ( condensateur C), donc fonctionnement en régime linéaire. AO1 : pas de boucle de contre réaction, donc fonctionnement en régime saturé.   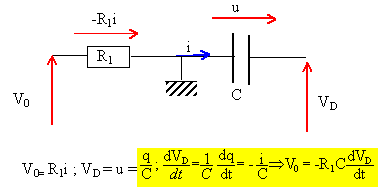Reconnaître les blocs du montage et en déduire le fonctionnement du dispositif ( nature des évolutions de VB et VD). Bloc autour de l'AO1: comparateur à hystérésis. VB prendra soit la valeur +Vsat soit la valeur -Vsat. Bloc autour de l'AO2: intégrateur inverseur : la présence des deux diodes D1 et D2 conduira à deux pentes. si VB = +Vsat la diode D1 est passante ; si VB = -Vsat la diode D2 est passante. L'intégration d'une fonction constante par intervalle va conduire à deux fonctions affines. si VB = +Vsat, VD = -R4 Vsat /R3 (VD décroissante). si VB = -Vsat, VD = R4 Vsat /R3(VD croissante). On s'intéresse à une phase de fonctionnement du montage pendant laquelle l'AO1 est en sortie haute : VB = V0 pour 0<=t < t1. En déduire que V0= -R1C dVD/dt. L'AO2 fonctionne en régime linéaire : les deux entrées sont au même potentiel, celui de la masse ( 0 V). VB est positif : la diode D1 est montée en direct ( diode passante), la diode D2 est montée en inverse ( diode bloquée). Initialement le condensateur est déchargé. Que vaut VD(t=0+) ? Trouver l'évolution de VD(t) pout 0 <=t <t1. VD(t=0+) =0 , condensateur déchargé. dVD/dt = -V0/(R1C) = constante. VD(t) = -V0/(R1C) t + Cte ; or VD(t=0+) =0 , donc la constante d'intégration est nulle. VD(t) = -V0/(R1C) t . Exprimer VA(t) . A quelle condition portant sur R3 et R4, l'AO1 peut-il basculer à t=t1 en sortie basse ? VA = (R3 VD+R4 V0) / (R3+R4 ). VA = V0 ( -R3/(R1C) t +R4 ) / (R3+R4 ). si VA devient négatif : e = V+ - V- = V+ - 0 = VA , e devient négatif et l'AO1 bascule en position basse. -R3/(R1C) t1 +R4 <=0 ; t1 = R4R1C /R3. On s'intéresse à la phase suivante du montage, après t1. En déduire que V0= R2C dVD/dt. L'AO2 fonctionne en régime linéaire : les deux entrées sont au même potentiel, celui de la masse ( 0 V). VB est négatif : la diode D2 est montée en direct ( diode passante), la diode D1 est montée en inverse ( diode bloquée). Trouver l'évolution de VD(t) après l'instant t1 et déterminer l'instant t2 de basculement. dVD/dt = V0/(R2C) = constante. VD(t) = V0/(R2C) t + Cte ; or VD(t=t1) =-V0R4/R3 , donc la constante d'intégration vaut : -V0R4/R3 = V0R4R1/(R2R3) + Cte ; Cte = -V0R4/R3 (1+R1/R2 ) VD(t) = V0/(R2C) t -V0R4/R3 (1+R1/R2 ). si VA devient positif : e = V+ - V- = V+ - 0 = VA , e devient positif et l'AO1 bascule en position haute. VD=-R4 V0/R3 = V0/(R2C) t2 -V0R4/R3 (1+R1/R2 ). R4/R3 (2+R1/R2)= 1/(R2C) t2 ; t2 = R4R2C/R3 (2+R1/R2). Le montage produit en régime établi des signaux périodique de période T = 2(t1+t2). T = 2[R4R1C /R3 + R4R2C/R3 (2+R1/R2)] ; T = 2R4C /R3[R1 +R2]. 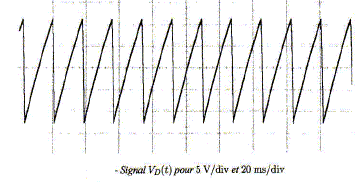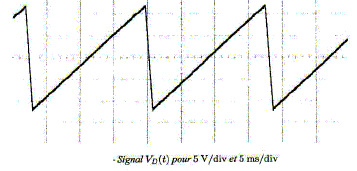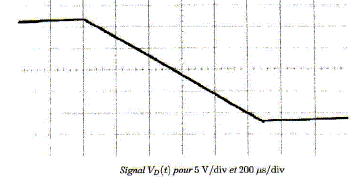Les figures suivantes sont des impressions d'écran d'oscilloscope ( pour diverses bases de temps) pour le signal VD(t). Sachant que V0 = 15 V, R4 = 82 kW et C = 0,1 mF, déterminer à partir des tracés les valeurs des résistances R1, R2, R3. Le deux premier tracé conduit à DV =4,8*5 = 24 V. Le second donne 2t2 = 3,3*5 10-3 = 16,5 10-3 s ; t2 =8,25 10-3 s Le dernier donne 2t1 = 5,5 * 200 10-6 ; t1 = 5,6 10-4 s. 24 = 2 R4 V0/R3 ; R3 = R4 V0/ 12 =82 103 *15/12 ; R3 =102,5 kW. t1 = R4R1C /R3 ; R1 =R3t1 /(R4 C) = 102,5 103*5,6 10-4/(10-7*82,5 103); R1 =7,0 kW. t2 = R4R2C/R3 (2+R1/R2) = 82 *R2*10-7/102,5*(2+7 103/R2)=8,3 10-3 ; 8 10-5 R2(2+7 103/R2)=8,25 ; 1,6 10-4 R2=8,25 -0,56 ; R2 =48 kW.

retour -menu