cinétique de dismutation de l'eau oxygénée : loi d'Arrhenius Concours Capes externe 2008

La dismutation du peroxyde d'hydrogène peut être catalysée par les cations Fe3+. Fe3+/Fe2+. E° = 0,77 V Ecrire l'équation de la réaction de dismutation. H2O2 = H2O + O2. Proposer une explication au rôle des ions Fe3+. Le potentiel 0,77 V du couple Fe3+ / Fe2+ est compris entre le potentiel du couple O2/ H2O2 (0,69 V) et celui du couple H2O2 /H2O (1,77 V). L'ion Fe3+ peut donc catalyser la réaction de dismutation de l'eau oxygénée. La réaction de dismutation lente est remplacée par deux réactions rapides où intervient Fe3+. Expliquer pourquoi les ions fer (II) peuvent aussi servir de catalyseur pour cette réaction. En présence d'ion Fe3+, oxydant, l'eau oxygénée se comporte comme un réducteur. En présence d'ion Fe2+, réducteur, l'eau oxygénée se comporte comme un oxydant. La réaction étant supposée d'ordre 1, établir la loi donnant la concentration en eau oxygénée en fonction du temps. d[H2O2] /dt = -k [H2O2] d[H2O2] / [H2O2] = -kdt ; d ln [H2O2] = -kdt. Intégrer entre t=0 et t : ln [H2O2]= - kt + Cste. à t = 0, ln [H2O2]0=Cste d'où : ln ([H2O2]0 / [H2O2] = kt.     On va atteindre la vitesse par mesure de pression dans un erlenmeyer fermé dans lequel on a introduit initialement les réactifs en présence d'air. La température est maintenue constante par un bain thermostaté. Pour chaque manipulation on introduit dans l'erlenmeyer 30,0 mL d'eau oxygénée à 0,25 mol/L, 20,0 mL d'eau et 3,0 mL de solution de cation Fe(III) à 0,037 mol/L. On ferme rapidement l'erlenmeyer tout en déclenchant l'acquisition de mesure de la pression. Le volume disponible pour la phase gazeuse a été mesuré : il est égal à 69,0 mL.L'expérience dont les résultats suivent a été réalisée à 20,3°C. DP mesure la variation de pression P(t)-P(t=0). Quantité de matière initiale d'eau oxygénée : n0 = 0,25*0,03 = 7,5 10-3 mol. avancement (mol) H2O2 =½O2 +H2O départ 0 n0 solvant en large excès en cours x n (H2O2) =n0-x n(O2) =½x On note V le volume du milieu réactionnel : vitesse de la réaction v= 1/V dx/dt. x = 2n(O2) ; n(H2O2) = n0-2n(O2) ; [H2O2] / [H2O2]0 = (n0-2n(O2)) /n0 = 1- 2 n(O2)/n0. Loi des gaz parfaits : n(O2) = DP V/(RT) d'où : [H2O2] / [H2O2]0 = 1- 2 DP V /(RTn0) V = 6,9 10-5 m3 ; T= 293,3K ; R = 8,32 J K-1 mol-1. 2V/(RTn0) = 2*6,9 10-5 /(8,32*293,3*7,5 10-3 )=7,54 10-6 Pa-1. ln [H2O2] / [H2O2]0 = ln (1-7,54 10-6DP) =- kt. 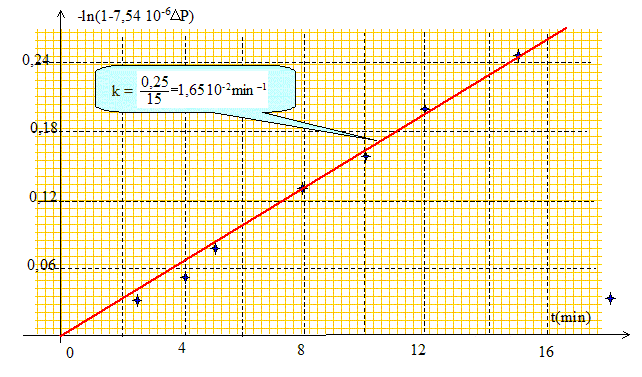On va tracer le graphe : -ln (1-7,54 10-6DP) =f(t)     Vérifier que ces résultats sont bien compatibles avec une cinétique d'ordre 1. t(min) 2,5 4,0 5,0 8,0 10,0 12,0 15,0 DP(Pa) 3900 7300 9600 16100 20000 23800 29200 1-7,54 10-6DP 0,97 0,945 0,928 0,879 0,849 0,820 0,780 -ln(1-7,54 10-6DP) 0,030 0,0565 0,0747 0,129 0,164 0,198 0,248 k = -ln(1-7,54 10-6DP) /t min-1 1,2 10-2 1,4 10-2 1,5 10-2 1,6 10-2 1,6 10-2 1,6 10-2 1,6 10-2   La courbe est une droite : l'hypothèse d'un ordre 1 est vérifiée. La même réaction a été réalisée à trois autres températures. 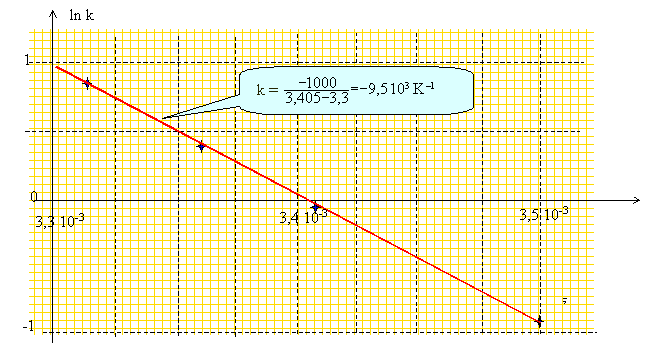On a obtenu les valeurs suivantes pour les constantes de vitesse : T(°C) 11,5 23,8 28,0 k(min-1) 0,0069 0,0244 0,0368 Quelle est la loi qui donne la variation de la constante de vitesse en fonction de la température ? loi d'Arrhenius. Quels sont ses critères d'utilisation ? Calculer l'énergie d'activation de cette réaction de décomposition de l'eau oxygénée. k = A exp (-EA/RT)  ; ln k = ln A - EA/(RT) On trace : ln k = f (1/T) T(°C) 11,5 20,3 23,8 28,0 1/T(K-1) 3,51 10-3 3,41 10-3 3,37 10-3 3,32 10-3 k(s-1) 0,0069*60 =0,411 0,99 1,46 2,21 ln k -0,889 -0,010 0,378 0,793 Par suite -EA/R = -9,5 103 d'où EA = 8,32*9,5 103 = 79 kJ mol-1.

retour -menu