Eau oxygénée : oxydoréduction ; diagramme E-pH ; potentiométrie Concours Capes externe 2008

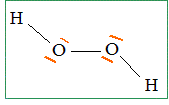
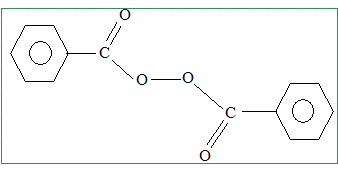
La molécule de peroxyde d'hydrogène ( eau oxygénée).  Donner les configurations électroniques des atomes d'oxygène et d'hydrogène dans leur état fondamental. H : 1s ; O : 1s2 2s2 2p4. Donner l'écriture de Lewis du peroxyde d'hydrogène. Donner deux exemples précis de molécules possédant l'enchainement -O-O-, les deux atomes d'oxygène étant liés par une liaison s. Proposer, pour chacun d'eux, une utilisation. 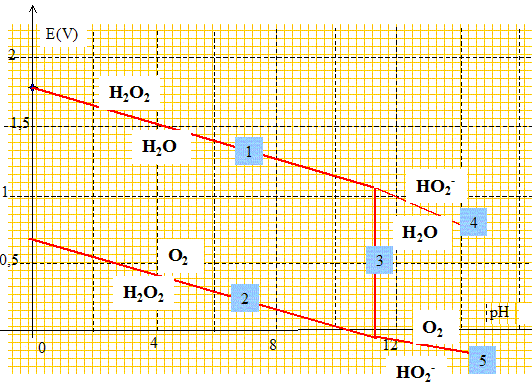Oxylite Na2O2 ( ion O22-) : en présence d'eau l'oxylithe donne du dioxygène Peroxyde de benzoyle : initiateur de radicaux libres. Solution d'eau oxygénée et oxydoréduction.  Ecrire les demi équations associées aux deux couples d'oxydoréduction faisant intervenir H2O2 et préciser le rôle de H2O2 dans chacun des cas. O2 /H2O2 : E° = 0,69 V. H2O2 = O2 +2H++2e- (1) : H2O2 joue le rôle de réducteur qui s'oxyde. H2O2 /H2O : E° =1,77 V. H2O2 +2H++2e- = 2H2O (2) : H2O2 joue le rôle d'oxydant qui se réduit. Sachant que H2O2 est la forme acide d'un couple acido basique de pKa = 11,6, écrire l'équation de la réaction de dissociation de cette forme acide en solution aqueuse. couple acide / base : H2O2 / HO2- : H2O2 + H2O = HO2- +H3O+. (3) Tracer à 25°C le diagramme potentiel-pH de l'eau oxygénée pour une concentration totale en solution de l'eau oxygénée de 0,10 mol/L et en prenant la pression du dioxygène égale à 0,20 bar. On demande les équations des différentes droites et l'allure du diagramme. (1) : E1 = 0,69 + 0,03 log (PO2 [H+]2 / [H2O2])  E1 = 0,69 + 0,03 log (PO2 / [H2O2])  +0,06 log [H+] E1 = 0,69 + 0,03 log (0,2 / 0,1)  -0,06 pH E1 = 0,70   -0,06 pH.   (2) : E2 = 1,77 + 0,03 log ( [H2O2] [H+]2 )  E2 = 1,77 + 0,03 log [H2O2]  +0,06 log [H+] E2 = 1,77 + 0,03 log (0,1)  -0,06 pH E2 = 1,74   -0,06 pH. (3) Ka =[HO2-][H3O+] /[H2O2] A la frontière [HO2-] = [H2O2] d'où pH= pKa = 11,6. HO2- = O2 +H++2e- (4) E4 = E°(O2/HO2-) + 0,03 log (PO2 [H+] / [HO2-])  Or E1 = 0,69 + 0,03 log (PO2 [H+]2 / [H2O2])  et [H2O2]=[HO2-][H3O+] /Ka E1 = 0,69 + 0,03 log (PO2 [H+] Ka / [HO2-] ) E1 = 0,69 -0,03 pKa +0,03 log (PO2 / [HO2-] )+0,03 log [H+] ( expression de E4) E4 = 0,69 -0,03*11,6 +0,03 log (0,2 / 0,1 )-0,03 pH E4 = 0,35-0,03 pH. HO2- +3H++2e- = 2H2O (5) E5 = E°(HO2-/H2O) + 0,03 log ( [H+]3 [HO2-])  Or E2 = 1,77 + 0,03 log ( [H2O2] [H+]2 )  et [H2O2]=[HO2-][H3O+] /Ka E2 = 1,77 + 0,03 log ( [HO2-] [H+]3 /Ka )   E2 = 1,77+0,03 pKa+ 0,03 log ( [HO2-] [H+]3 ) ( expression de E5) E5 = 1,77 +0,03*11,6 + 0,03 log 0,1  -0,09 pH. E5 = 2,09 -0,09 pH.    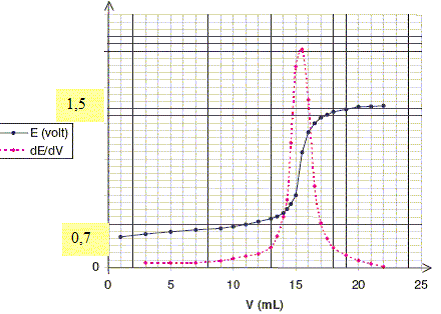L'observation de ce tracé vous permet-il de conclure quant à la stabilité thermodynamique des solutions d'eau oxygénée. L'eau oxygénée va se dismuter en O2 et H2O. On trouve en pharmacie des solutions d'eau oxygénée portant l'indication eau oxygénée 10 volumes. Interpréter cette indication. Le titre d'une eau oxygénée exprime le volume de dioxygène (mesuré en L dans les conditions normales de température et de pression) que peut libérer un litre d'eau oxygénée. Calculer l'ordre de grandeur de la concentration de la solution d'eau oxygénée. H2O2 = ½O2 + H2O d'où n(H2O2) = 2 n(O2) =2 *10/22,4 = 0,89 mol dans 1 L. Comment peut-on expliquer l'existence de telle solution commerciale ? La réaction de décomposition de l'eau oxygénée à l'abri de la lumière ( flacon opaque) et à température peu élevée est très lente. Les solutions d'eau oxygénée peuvent être dosées par manganimétrie, le dosage étant suivi par potentiométrie. Ecrire l'équation de dosage et vérifier que la réaction est quantitative. MnO4-/Mn2+ : E° = 1,51 V. 2 fois {MnO4- + 8H+ +5e- =Mn2++ 4H2O} (6) O2 / H2O2 : E° = 0,69 V. 5 fois { H2O2 = O2 + 2H+ +2e-}(7) 2 MnO4- + 6H+ +5H2O2 --> 2 Mn2++ 5O2 +8H2O (8) K = [Mn2+]2[O2]5/ ([H2O2]5[H+]6[MnO4-]2) (6) : E6 = 1,51 + 0,06/5 log ([MnO4-][H+]8/[Mn2+]) (7) E7 =0,69 +0,03 log ([H+]2[O2]/[H2O2]) A l'équilibre E6 = E7 ; 1,51-0,69 = 0,03 log ([H+]2[O2]/[H2O2]) - 0,06/5 log([MnO4-][H+]8/[Mn2+]) 0,82 = 0,006 log ([O2]5[H+]10/[H2O2]5)- 0,006 log ([MnO4-]2[H+]16/[Mn2+]2) 0,82/ 0,006 = log ([O2]5 [Mn2+]2 /([MnO4-]2[H+]6[H2O2]5) ) ; 136,7 = log K ; K = 4 10136. La constante K étant grande, la réaction est quantitative. Quelle est la couleur de la solution avant l'équivalence, après l'équivalence ? La seule espèce colorée est l'ion permanganate ( violet) ; avant l'équivalence, dans le bécher, l'ion permanganate est en défaut : la solution est incolore. Après l'équivalence l'ion permanganate est en excès : la solution devient rose violette. On a mis dans le bécher 10,0 mL de solution d'eau oxygénée auxquels on a ajouté 85 mL d'eau, 5 mL d'acide sulfurique concentré ( on veut pH=0). L'équivalence est obtenue pour un volume versé de 17,0 mL de solution de permanganate de potassium à 0,020 mol/L. Calculer la concentration de la solution d'eau oxygénée. D'après (8) : n( H2O2) = 2,5 n(MnO4-) = 2,5 * 17,0 10-3 *0,020 = 8,5 10-4 mol. [H2O2] = 8,5 10-4 /0,01 = 8,5 10-2 mol/L. Cette solution a été obtenue en diluant 10 fois la solution commerciale. Que peut -on dire de la solution mère ? [H2O2] mère=  10 * 8,5 10-2 = 0,85 mol/L. Cette valeur est très proche de 0,89 mol/L : la solution mère a été fraichement préparée et la dismutation de l'eau oxygénée est peu avancée. Quelles sont les électrodes nécessaires pour suivre le dosage ? Préciser le rôle de chacune d'elles ?  L'électrode de référence utilisée ici est une électrode au calomel saturée (ECS), c'est à dire une électrode de platine (Pt) recouverte de mercure (Hg) sur lequel est déposé du calomel Hg2Cl2. Cette électrode est dite saturée car la solution dans laquelle plonge l'électrode ainsi constituée est une solution aqueuse saturée en chlorure de potassium KCl. Une électrode de mesure en platine par exemple. Décrire une électrode classiquement utilisée en TP comme électrode de référence. Ecrire la demi-équation ox/red correspondant au couple utilisé et montrer que son potentiel est constant. couple Hg2Cl2 (s)/ Hg (l) : Hg2Cl2 (s)+ 2e- =2 Hg(l) + 2Cl-. Eréf = E°[ Hg2Cl2 (s)/ Hg (l)] + 0,03 log 1/[Cl-]2. Eréf = 0,27 -0,06 log [Cl-]. Dans la solution saturée en KCl : [Cl-] = 4,7 mol/L à 25 °C. E réf = 0,27 -0,06 *log 4,7 = 0,23 V.   Donner ( en négligeant la dilution) l'expression du potentiel en fonction du volume V versé ( V exprimé en L) avant l'équivalence, à l'équivalence, après l'équivalence. 2 MnO4- + 6H+ +5H2O2 --> 2 Mn2++ 5O2 +8H2O Le tableau d'évolution est construit d'après le mélange initial hypothétique n(H2O2 ) = n et n(MnO4-) = n0. On note V le volume de solution de permanganate ajouté. avancement (mol) 2 MnO4- + 6H+ +5H2O2 --> 2 Mn2+ + 5O2 +8H2O initial 0 n0 en excès n 0 0 solvant en large excès avant équivalence x = CV n0 - 2CV n-5CV 2CV 5 CV à l'équivalence CVE n0 - 2CVE 0 2CVE 5CVE après l'équivalence CV C(V-VE) 0 2CVE 5CVE Avant l'équivalence, MnO4- est en défaut, la solution contient les espèces O2 et H2O2 : le couple ox/red O2 / H2O2 fixe le potentiel. E =0,69 +0,03 log ([H+]2[O2]/[H2O2]) avec pH=0 = constante. [O2] = 5C ; [H2O2] = (n - 5CV) / V. E =0,69 +0,03 log ([O2]/[H2O2]) = 0,69 + 0,03 log (5CV/(n - 5CV) ) A l'équivalence, la solution contient les espèces Mn2+ et O2 : on mesure un potoentiel mixte peu stable O2/Mn2+ Eéq =(5*1,51 + 2*0,69) / 7 = 1,28 V. Après l'équivalence, H2O2 est en défaut, la solution contient les espèces MnO4- et Mn2+ : le couple ox/red MnO4- / Mn2+ fixe le potentiel. E =1,51 +0,012 log (([MnO4-][H+]8/[Mn2+]) avec pH=0 = constante. [MnO4-] = C(V-VE) / V ; [Mn2+] = 2CVE / V. E =1,51 +0,012 log ((V-VE)/(2VE )). Donner l'allure du graphe E=f(V).

retour -menu