thermodynamique : transformations d'un gaz parfait BTS travaux publics 2008.

On considère un gaz parfait initialement dans l'état A ( PA= 105 Pa ; TA = 273 K ; VA =50 L). On amène ce gaz dans l'état C ( PC= 10 PA ; TC ; VC ) de deux manières différentes : transformation (1) : compression adiabatique de l'état A à l'état C transformation (2) : compression isotherme de l'état A à l'état B puis échauffement à pression constante , de l'état B à l'état C. Le système est considéré comme fermé et touts les transformations sont réversibles. Calculer le nombre de moles, noté n, de gaz mis en jeu. Ecrire l'équation des gaz parfaits dans l'état A : PV = nRT. P : pression en pascal ; V : volume (m3) ; n : quantité de matière (mol) ; T : températuer (K) ; R =8,31 J mol-1 K-1. n = PV RT = 105 * 50 10-3 8,31*273 = 2,2 mol On garde une valeur plus précise pour la suite des calculs : 2,204 mol   Calculer les variables d'états inconnues ( température et volume) dans l'état C lorsque la masse de gaz subit la transformation (1) : On donne : g = 1,4 ; 1/ g =0,714 adiabatique réversible PAVAg = PCVCg . VC =VA [ PA PC ]1/g = 50 10-3[0,1]0,714 ~ 9,7 10-3 m3 On garde une valeur plus précise pour la suite des calculs : 9,656 10-3 m3. Puis écrire l'équation des gaz parfaits en C : TC = PCVC nR = 10 105 * 9,656 10-3 2,204*8,31 = 527 K Préciser la température et la pression du gaz dans l'état B ( transformation n°2). Puis calculer VB. A---> B : compression isotherme TA=TB = 273 K. B---> C: isobare : PC=PB = 10 PA = 106 Pa. 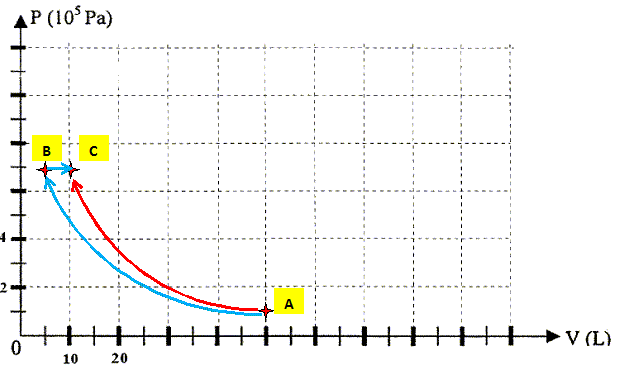Puis écrire l'équation des gaz parfaits en B : VB = nR TB PB = 2,204*8,31*273 106 = 5,0 10-3 m3 variables A B C P(Pa) 1 105 10 105 10 105 V(L) 50 5 9,7 T(K) 273 273 527   Représenter les transformations 1 et 2 sur un diagramme (P,V). Le travail échangé - entre les états A et C lors de la transformation 1 est W1 = 1,16 104 J. - entre les états A et B lors de la transformation 2 est WAB = 1,15 104 J. Que peut-on dire d'une transformation adiabatique ? Lors d'une transformation adiabatique, il n'y a pas d'échange de chaleur avec le milieu extérieur : Q1 = 0. Calculer lors de la transformation 2, le travail WBC des forces de pression. Transformation isobare donc WBC = -P(VC-VB) = -106 (9,7 10-3 - 5 10-3) = -4,7 103 J. En déduire le travail W2 échangé sur lensemble de la transformation 2. W2 = WAB + WBC= 1,15 104 - 4,7 103 = 6,8 103 J. Exprimer et calculer la quantité de chaleur QAB et la quantité de chaleur QBC mises en oeuvre lors de la transformation 2. En déduire Q2. On donne CP = 29,1 J mol-1 K-1. A---> B isotherme : la variation d'énergie interne du gz est nulle d'où QAB + WAB = 0  QAB =- WAB = -1,15 104 J. B---> C isobare d'où QBC = nCP(TC-TB) = 2,2*29,1(527-273) = 1,63 104 J. Q2 = QAB +QBC = -1,15 104 + 1,63 104 = 4,76 103 J. Calculer alors les variations d'énergie internes DU1 et DU2. Que vérifie t-on ? DU1 = W1 + Q1 = 1,16 104 J. DU2 = W2 + Q2 =6,8 103 +4,76 103 = 1,16 104 J. DU1 =DU2 : l'énergie interne est une fonction d'état ; sa variation ne dépend que de l'état initial A et final C, peut importe le chemin suivi, 1 ou 2.

retour -menu