Tuyaux sonores bac S Amérique du Nord 2008. voir le site du lycée Rochambeau

LLa célérité du son dans l'air est v=340 m/s à 15°C. Ondes sonores. Une onde sonore émet un son continu dans l'air. Caractériser l'onde sonore qui se propage dans l'air en utilisant tout ou partie du vocabulaire suivant : progressive, électromagnétique, transversale, mécanique, longitudinale, stationnaire. Onde mécanique progressive longitudinale. Un auditeur peut déterminer la direction dans laquelle est située une source sonore S, sans la voir, quand le retard entre les vibrations reçues par ces deux oreilles D(droite) et G (gauche) est au moins égal à 1,0 10-4 s. L'auditeur pourra t-il définir la direction de la source sonore S si celle-ci est située à 7,20 m de son oreille droite et à 7,10 m de son oreille gauche, la température étant 15°C ? Distance DG = 0,10 m ; célérité du son dans l'air à 15°C : v= 340 m/s. Le retard entre les vibrations est Dt = DG/v = 0,10 /340 = 2,94 10-4 s. Cette valeur est supérieur à 1,0 10-4 s : l'auditeur peut donc définir la direction de la source. Tuyaux sonores à embouchure de flûte. Les tuyaux sonores à embouchure de flûte équipent en partie les tuyaux d'orgues. Un tuyau sonore à embouchure de flûte, comprend un biseau : l'air vient frapper ce biseau, il en découle une mise en oscillation de la colonne d'air à l'intérieur du tuyau. Ces tuyaux sont considérés comme des tuyaux ouverts au niveau de l'embouchure. L'autre extrémité du tuyau peut être : - soit ouverte, le tuyau sonore est alors un tuyau ouvert aux deux extrémités. - soit fermée, le tuyau est alors ouvert à une extrémité, fermé à l'autre. A une extrémité ouverte est toujours situé un ventre de vibration noté V ; à une extrémité fermée est toujours situé un noeud de vibration noté N. Tuyau sonore ouvert aux deux extrémités. Un tuyau sonore de longueur L ouvert aux deux extrémités émet à q=15°C un son de fréquence f=262 Hz. L'état vibratoire du mode fondamental du tuyau peut être représenté de la manière suivante : A quel type d'onde appartient le mode de vibration de la colonne d'air ? Ondes stationnaires. Parmi les caractéristiques suivantes d'un son, quelle est celle qui correspond à la fréquence du son ? intensité, hauteur, timbre. La hauteur correspond à la fréquence. Dans le cas d'une corde tendue entre deux points fixes, donner la relation entre la distance qui sépare deux ventres ou deux noeuds succsssifs en fonction de la longueur d'onde. Deux ventres ou deux noeuds successsifs sont distants d'une demi longueur d'onde ½l. Sachant qu'elle reste valable dans le cas du tuyau sonore, en déduire la relation entre L, v et f. Justifier l'affirmation suivante : " à un tuyau sonore long correspond un son grave" f = v/(2L) : la fréquence est inversement proportionnelle à la longueur L. Si L est grand, la fréquence est faible : une fréquence faible correspond à un son grave. 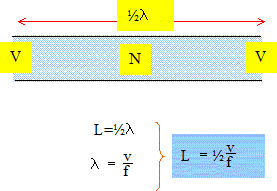Exprimer en fonction de f, la longueur L2 du tuyau qui émettrait un son dont le fondamental correspondrait à l'harmonique de rang 2 du tuyau de longueur L. La fréquence f2 de l'harmonique de rang 2 est égale à f2= 2f. L2 = ½v/f2 = v/(4f). En déduire la relation entre L et L2. L = v/(2f) et L2 =v/(4f) d'où L2 =½L. Tuyau sonore fermé à une extrémité. Soit un tuyau à embouchure de flute de longueur L0, mais fermé à l'autre extrémité. Ce tuyau est représenté ci-dessous dans le mode fondamental. Par analogie avec une corde tendue entre deux points fixes, exprimer la fréquence f0 en fonction de v et L0. Un élève affirme :" un tuyau ouvert aux deux extrémités sonne avec une fréquence double de celle du tuyau de même longueur, fermé à une extrémité ". Vrai ou faux ? Justifier. Fréquence du mode fondamental du tuyau ouvert aux deux extrémités f = v/(2L). Fréquence du mode fondamental du tuyau de même longueur ouvert à une extrémité f ' = v/(4L). D'où f = 2f 'et l'affirmation est vraie.    Influence de la température sur la fréquence du son émis.  La vitesse du son dans l'air est proportionnelle à T½. T est la température absolue en kelvin (K) ; elle est reliée à la température q en degré Cesius par : T = 273,15 +q. Expérience : La longueur du tuyau sonore est L. On rappelle la fréquence du son émis à q=15°C ; f = 262 Hz. On réalise une nouvelle expérience au cours de laquelle la température de l'air a augmenté de 7°C ; la vitesse du son est devenue v' et la fréquence f '. Exprimer la vitesse v du son dans l'air à la température T. v = l f avec f = A T½ ( A étant une constante) Par suite : v = Al T½ (1) Exprimer la vitesse v' du son dans l'air à la température T'. En déduire l'expression de v' en fonction de T, T' et v. v' = Al T '½. Or d'après (1) Al= v T-½ d'où : v' = v [T ' / T]½. (2) Montrer que la nouvelle fréquence f' du son à la tempéreture T ' est donnée par la relation : f ' = [T ' / T]½ f. f= v/l ; f '= v '/l d'où : f ' / f = v ' / v soit f ' = v ' / v f. Et en tenant compte de (2) : f ' = [T ' / T]½ f. Une oreille moyenne distingue deux sons de fréquence f et f ' si le rapport log ( f ' / f) est supérieur à 5 10-3. L'oreille moyenne pourra t-elle distinguer les deux sons émis avec un écart de température de 7°C ? T = 273,15 +15 = 288,15 K ; T ' = 273,15+22 = 295,15 K [T ' /T]½ =[295,15 / 288,15]½ =1,012. Par suite f '/f = 1,012 et log ( f ' / f) =5,21 10-3 ~ 5 10-3. Cette valeur étant très proche de 5,0 10-3, l'oreille moyenne aura bien du mal à distinguer les deux sons émis.

retour -menu