Mécanique fluidique bac STL physique de laboratoire et procédés industriels 2008.  Oscillateur mécanique ; onde progressive et onde stationnaire ; débitmètre.

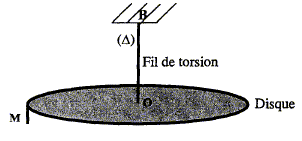
Etude d'un oscillateur mécanique (4 points)  L'oscillateur est constitué d'un disque homogène de masse m, situé dans un plan horizontal et fixé en son centre O à un fil de torsion vertical de constante de torsion C dont l'extrémité B est fixe. On écarte le disque de sa position d'équilibre en le faisant tourner horizontalement d'un angle qm autour de son axe de rotation OB, puis on le lâche sans vitesse initiale. Le disque effectue alors des oscillations autour de sa position d'équilibre. Un repère M de masse négligeable est fixé sur la périphérie du disque. On appelle q l'angle que fait le disque avec sa position d'équilibre à chaque instant du mouvement. Le moment d'inertie du disque est noté ID. 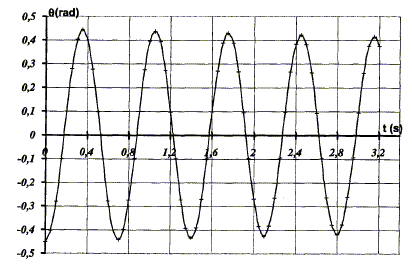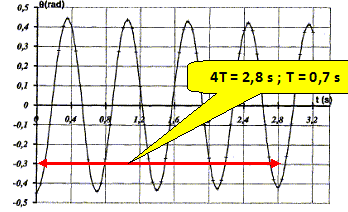Un dispositif permet d'enregistrer à l'ordinateur les positions successives de M. La courbe obtenue est donnée ci-dessous.   Déterminer graphiquement la valeur de la pseudo-période T des oscillations mécaniques. Etablir que l'équation différentielle de l'oscillateur ( dans le cas où les frottements sont négligés) est : q" + C/ID q =0. On suppose que la somme des moments qui s'appliquent au disque se réduit au moment du couple de torsion dû au fil. Moment du couple de torsion ( couple de rappel : -Cq. Le théorème du moment cinétique appliqué à un solide en rotation autour d'un axe fixe s'écrit : -Cq = IDq" ; IDq" + Cq = 0 ; q" + C/ID q =0. Déduire de l'équation précédente, l'expression de la période propre T0 en fonction de C et ID. w0 =(C/ID)½ ; de plus w0 = 2p /T0 ; T0 = 2p /w0 ; T0 = 2p (ID/C)½. On assimile la période propre T0 à la pseudo-période T. Calculer ID si C = 4,0 10-2 SI et préciser son unité. T2 = 4 p2 ID / C ; ID = T2 C / (4 p2) ID = 0,72*0,04 /(4*3,142) =4,96 10-4 ~ 5,0 10-4 kg m2. Donner l'expression de l'énergie mécanique Em de cet oscillateur en fonction des énergies potentielle et cinétique. Em = Energie cinétique + énergie pototentielle Em = ½ ID w2 + ½Cq2. Quelle est la valeur de l'énergie cinétique de l'oscillateur quand l'angle q est égal à l'amplitude des socillations q m = 0,45 rad. En déduire la valeur de l'énergie mécanique. L'énergie cinétique est nulle ( disque à l'arrêt ) ; l'énergie mécanique est sous forme d'énergie potentielle : Em = ½Cq2m = 0,5*0,04*0,452 =4,1 10-3 J. Onde progressive et onde stationnaire. 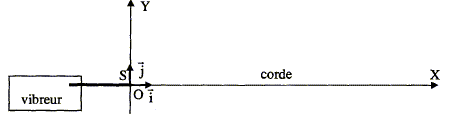Une onde progressive sinusoïdale se propage sans perte d'énergie le long d'une corde tendue avec la célérité v = 15 m/s. Chaque point de la corde est repéré par son abscisse x et son ordonnée y. 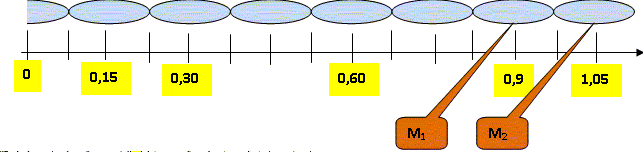L'élongation de la source S, exprimée en mm, s'écrit : yS(t) = 4 sin (100pt), t exprimé en seconde. Onde progressive. Donner la valeur numérique de la pulsation w de l'onde, de sa période T en précisant les unités et montrer que la longueur d'onde l est égale à 0,30 m. w = 100 p = 314 rad/s. T = 2 p /w =0,02 s. l = v T = 15*0,02 =0,30 m. On considère le point M1 de la corde d'abscisse x1 =0,90 m. Montrer que l'amplitude du point M1 à l'instant t est celle qu'avait la source à l'instant t-x1/v.  Le point M1 reproduit le mouvement de la source S avec un retard q = x1/v = 0,90/15=0,06 s. yM1(t) = yS(t-q )= yS(t- x1/v ). En déduire que l'équation hotaire du mouvement de M1 s'écrit : yM1(t) = 4 sin(100p t - 6p). yM1(t) = yS(t-q )= yS(t- 0,06 ) = 4 sin (100p(t-0,06)) = 4 sin (100p t -6p). Déterminer la différence de phase Dj entre la source S et M1 à la date t ? La fonction sinus est périodique de période 2p : sin x =sin (x + 2kp) par suite yM1(t) = 4 sin (100p t ) = yS(t) Les points S et M1 se trouvent dans le même état vibratoire ; S et M1 vibrent en phase et Dj =0. L'onde progressive atteint ensuite le point M2 tel que M1M2 = 15 cm. Donner la relation qui existe entre la distance M1M2 et la longueur d'onde, comparer alors les mouvements de M1 et M2. M1M2 = 0,15 m = ½l. Les points M1 et M2 vibrent donc en opposition de phase. Onde stationnaire. On appuie sur la corde à la distance L= 1,125 m de la source, cet obstacle provoque la réflexion de l'onde issue de la source S. Une onde sinusoïdale de même amplitude 4 mm, de même pulsation w se propage en sens opposé à l'onde incidente et on étudie le phénomène qui rsulte de leur superposition. Décrire en quelques mots le phénomène observé. L'extrémité fixe est un noeud de vibration ; l'extrémité libre ( S) est un ventre de vibration. Observée à l'aide d'un stroboscope, la corde prend l'aspect d'un ou plusieurs fuseaux. - les extrémités d'un fuseau sont immobiles : noeuds de vibration. - le milieu d'un fuseau vibre avec une amplitude maximum : ventre de vibration. La longueur d'onde l étant prise égale à 30 cm, dessiner l'aspect de la corde à un instant quelconque. L = 1,125 m ; 1,125/0,3 = 3,75 l. Le point M1, d'abscisse x1 = 90 cm est-il un noeud ou un ventre de vibration ? Qu'en est'il du point M2 ? 0,90 /0,3 = 3 l : M1 est un ventre de vibration. 0,90+0,15 = 1,05 = 3,5 l : M2 est un ventre de vibration. 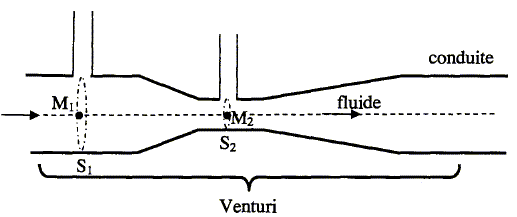Débitmètre. (3,5 points) Un tube de venturi est constitué d'un convergent et d'un divergent reliés par un col. On intercale le tube dans une conduite où circule un fluide parfait supposé imcompressible de masse volumique r et dont on veut mesurer le débit Qv. Sur ce tube sont installées deux prises de pression statique. S1 et S2 sont les sections droites de la conduite à l'endroit des prises de pression et S1/ S2 =2 ; v1 et v2 sont les vitesses du fluide respectivement en M1 et M2 ; p1 et p2 sont les pressions statiques du fluide respectivement en M1 et M2. Comparer v1 et v2 ; en déduire le rapport des vitesses v1/v2. Justifier. Le débit volumique se conserve : Qv = S1v1 = S2v2 ; v1 /v2 = S2/S1=0,5.  v2 est égale à 2 fois v1. Le tube de Venturi est horizontal. Ecrire le théorème de Bernoulli entre les points M1 et M2 puis comparer p1 et p2 sans effectuer de calculs. p1 + ½rv12 =p2 + ½rv22 . or v22 = 4 v12 ; ½rv22 = 4 .½rv12 ; donc p2 < p1. Etablir l'expression Dp = p1-p2 en fonction de r, v1 et v2.  p1-p2 =½r(v22 - v12 ). Le régime d'écoulement du fluide est permanennt ; déterminer l'expression de Dp en fonction de r, Qv, S1 et S2. v2 = Qv/S2 ; v1 = Qv/S1 ; Dp = ½r Q2v(1/S22-1/S21 ). Calculer Qv. r = 900 kg m-3 ; Dp= 0,36 kPa ; S1 = 30 cm2. Dp= 360 Pa ; S1 = 3. 10-3 m2 ; S2 = 1,5. 10-3 m2. 1/S22-1/S21=106(1/1,52-1/32) =3,33105 ; ½r = 450. Qv2 = 360/(450*3,33 105) =2,4 10-6 ; 1,55 10-3 ~ 1,5 10-3 m3 s-1.

retour -menu