Electricité bac STL physique de laboratoire et procédés industriels 2008.  Balance électronique : transformateur, redressement, pont de Wheatstone, AO régime linéaire.

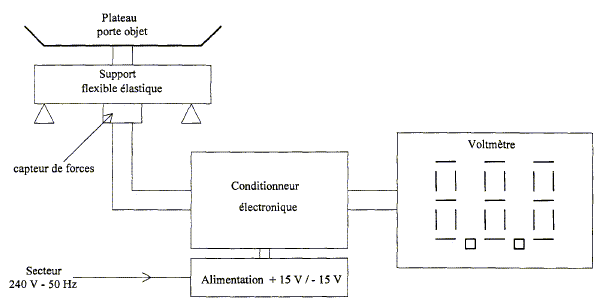
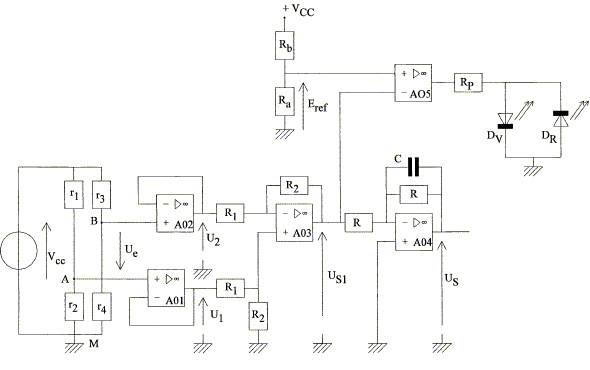
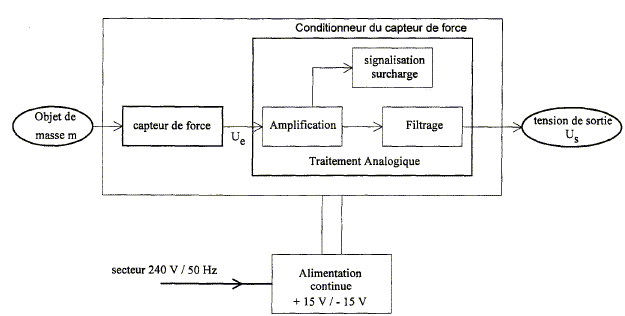
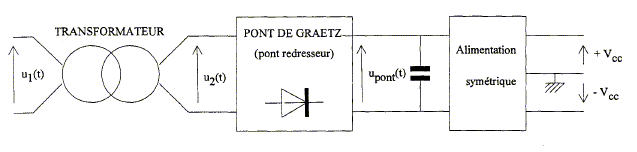
ce problème propose une étude simplifiée d'une partie des fonctions rencontrées dans une balance électronique destinée à peser des objets de masse m. Cette balance est alimentée par le secteur 240 V - 50 Hz. Schéma de principe. Synoptique : Etude de l'alimentation de la balance. Les amplificateurs opérationnels (AO) sont alimentés par une alimentation délivrant deux tensions symétriques +Vcc = +15 V et -Vcc =-15 V. Ces deux tensions sont obtenues à partir de la tension u1(t) issue du réseau de distribution.   Etude du transformateur (2 points). 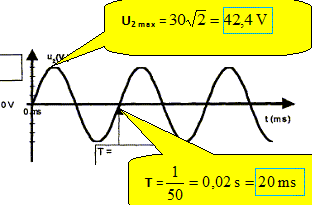Le transformateur est supposé parfait, on lit sur sa plaque signalétique les grandeurs suivantes : 240 V / 30 V ; 50 Hz ; 48 V A. A quoi correspondent ces différentes grandeurs ? 240 V : tension efficace au primaire ; 30 V : tension efficace à la sortie du secondaire. 50 Hz : fréquence de la tension alternative ; 48 VA : puissance apparente. Calculer le rapport de transformation du transformateur. m = 30/240 = 0,125. Déterminer les intensités efficaces nominales I1N et I2N des courants primaire et secondaire. I1N = 48/240 = 0,2 A. I2N = 48 / 30 = 1,6 A. Etude de la tension redressée (2 points). le transformateur est alimenté par le réseau de distribution 240 V - 50 Hz. Quelle est la valeur efficace de la tension à l'entrée du pont redresseur ? Comment peut-on la mesurer ? ( nom de l'appareil et mode de mesure) 30 V : tension au secondaire du transformateur. La mesure est réalisée à l'aide d'un voltmètre électronique sur la position AC. Compléter les valeurs de T, période du signal, et de U2max sur le document suivant, qui représente l'allure de la tension u2(t) à l'entrée du pont de Graetz. Représenter l'allure de la tension upont(t) à la sortie du pont de Graetz dans le cas d'une charge purement résistive. Représenter l'allure de la tension upont(t) à la sortie du pont de Graetz dans le cas d'une charge RC parallèle. 2è partie. 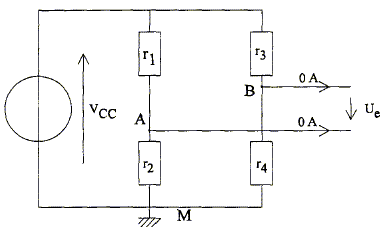Schéma général : Etude du pont de jauge : (3 points) Le capteur de forces est constitué de jauges de contraintes dont la résistance r varie avec la force F à laquelle il est soumis suivant la relation : Dr / r = k F avec D r : variation de la résistance ; k = 4 10-4 N-1. Ces jauges sont disposées selon un pont de Wheatstone alimenté par la tension +Vcc = 15 V. r1=r4=r-Dr ; r2=r3=r+Dr. 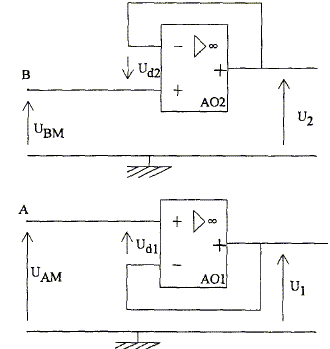Exprimer UAM en fonction de r1, r2 et Vcc. On note i l'intensité du courant dans r1 et r2 : Vcc = r1 i + r2 i soit i = Vcc/(r1+r2). UAM = r2 i = Vcc r2 /(r1+r2). Exprimer UBM en fonction de r3, r4 et Vcc. On note i' l'intensité du courant dans r3 et r4 : Vcc = r3 i' + r4 i' soit i' = Vcc/(r3+r4). UBM = r4 i' = Vcc r3 /(r3+r4). En déduire UAM puis UBM en fonction de r, Dr et Vcc. r1+r2= 2r ; r2=r+Dr ; UAM =Vcc (r+Dr) / (2r). r3+r4= 2r ; r4=r-Dr ; UBM =Vcc (r-Dr) / (2r). Exprimer Ue en fonction de UAB, puis de r, Dr et Vcc. Ue = UAB = UAM+UMB = UAM-UBM ; Ue = Vcc Dr/ r. Montrer que Ue peut se mettre sous la forme Ue = a m. avec a = k g Vcc ( m représente la masse de l'objet et g l'intensité du champ de pesanteur )  Dr / r = k F avec F= m g ( poids de l'objet) ; Ue = k g Vcc m = a m. Calculer a et préciser son unité ( prendre g= 10 N kg-1) a = k=4 10-4 N-1 ; Vcc = 15 V ; a = 4 10-4 *10*15 =0,06 V kg-1. Que vaut Ue en l'absence d'objet sur le plateau ? m=0 ; Ue= a m = 0. Etude des montages suiveurs (AO1 et AO2) : (1 point ) Quelle est le régime de fonctionnement des AO1 et AO2 ? Justifier. La présence d'une boucle de contre réaction ( liaison entre la sortie et l'entrée inverseuse ) conduit à un régime linéaire. Exprimer U1 en fonction de UAM et U2 en fonction de UBM. Montage suiveur, donc U1=UAM et U2= UBM. Quel est l'intérêt d'un montage suiveur ? Impédance d'entrée infinie et impédance de sortie nulle ; U1 et U2 sont indépendant des courants dans les branches AM et BM. Etude du montage soustracteur (AO3) : (4 point ) Cet étage permet d'amplifier la différence U1-U2. 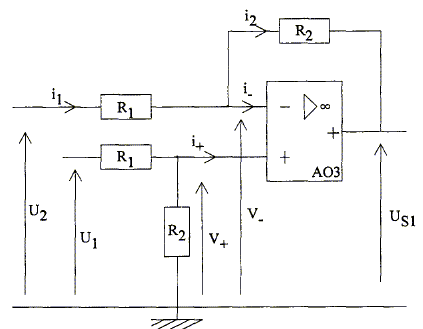L'AO étant parfait quelles sont les valeurs des intensités i+ et i- ? i+ = i- = 0. Quel est le régime de fonctionnement de l'AO ? Justifier. La présence d'une boucle de contre réaction ( liaison entre la sortie et l'entrée inverseuse R2) conduit à un régime linéaire. Exprimer V+ en fonction de R1, R2 et U1. On note i l'intensité dans R1 et R2 : U1 = R1i+ V+ et i = V+/R2. U1 = R1V+/R2 + V+ ; V+= U1 / ( 1+R1/R2). Exprimer i1 en fonction de U2, V- et R1. U2= V-+ R1i1 ; i1 = (U2- V-) / R1. Exprimer i2 en fonction de US1, V- et R2. US1+R2 i2= V- ; i2= (V-- US1)/R2. Exprimer i1 en fonction de i2, puis en déduire Us1 en fonction de R1, R2, V- et U2. i1 = i2 ( car i-=0) ; (U2- V-) / R1 = (V-- US1)/R2 ; (U2- V-) R2 / R1 =V-- US1. US1= V--(U2- V-) R2 / R1= V-( 1+R2 / R1) -R2 / R1U2. Montrer que US1 = R2/R1(U1-U2) ; en déduire que US1= R2/R1 a m. V+ = V- ( régime linéaire) ; V-= U1 / ( 1+R1/R2). US1=V-( 1+R2 / R1) -R2 / R1U2 = U1 ( 1+R2 / R1)/( 1+R1/R2) -R2 / R1U2 =U1 R2 / R1-R2 / R1U2 ; US1=R2 / R1(U1-U2) ; or UAM-UBM = am et UAM-UBM =U1-U2 ; US1= R2/R1 a m. Déterminer la relation entre R1 et R2 qui permettrait d'obtenir US1 = 10 V pour m = 100 kg. 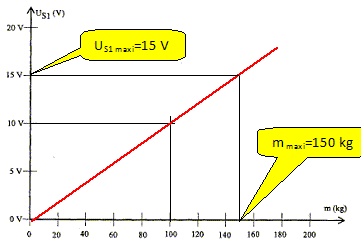a = 0,06 V kg-1 ;  R2/R1 = US1/(am) =10/(0,06*100) =10/6 ; R2/R1 =5/3 = 1,67. Tracer la courbe US1 = f(m) pour une masse comprise entre 0 et 200 kg. En déduire la masse maximum que l'on peut peser. US1= 5/3*0,06 m =0,3/3 m ; US1= 0,1 m.

retour -menu