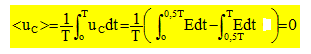Onduleur, moteur asynchrone triphasé, énergie, puissance bac STI génie mécanique 2008.

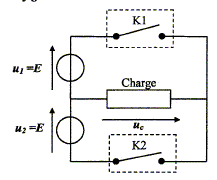
Partie A : questions de cours. Quel dispositif permet de réaliser une conversion alternatif / alternatif sinusoïdale 15 kV / 3300 V ? Transformateur abaisseur de tension. Quel type de convertisseur permet d'obtenir une tension continue à partir d'une tension sinusoïdale de 3300 V ? Redresseur : pont de Graëtz + bobine de lissage en série. Quel type de convertisseur permet d'obtenir une tension continue variable à partir d'une tension continue fixe ? Hacheur. Partie B : étude d'un onduleur. La tension en entrée des onduleurs est continue. 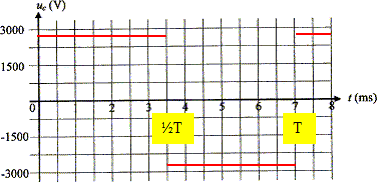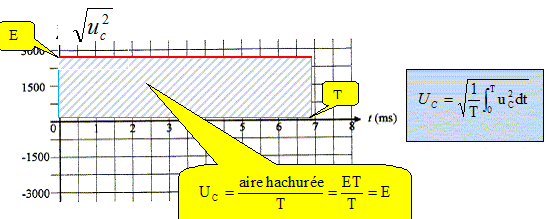On considère un onduleur monophasé à deux interrupteurs dont le schéma de principe est donné ci-dessous : K1 et K2 sonr deux interrupteurs électroniques commandables à l'ouverture et à la fermeture. E = 2750 V. les interrupteurs sont fermés et ouverts de façon périodique en respectant la règle suivante : - pour t appartenant à [0 ;½T[ , K1 est fermé et K2 est ouvert. - pour t appartenant à [½T ; T[ , K1 est ouvert et K2 est fermé. Calculer la période T de fonctionnement de l'onduleur si la fréquence est f =140 Hz. T=1/f = 1/140 T=7,14 10-3 s Calculer uC en fonction de E sur une période. - pour t appartenant à [0 ;½T[ , K1 est fermé et K2 est ouvert : uC= u1=E. - pour t appartenant à [½T ; T[ , K1 est ouvert et K2 est fermé : uC= -u2=-E. Tracer la tension uC aux bornes de la charge pour une fréquence de fonctionnement correspondant à une période T= 7 ms. Calculer la fréquence correspondante. T = 7 10-3 s ; f = 1/T = 1/ 710-3 = 1000/7 =143 Hz. Déterminer la valeur moyenne <uC> de la tension aux bornes de la charge. Justifier brièvement. - pour t appartenant à [0 ;½T[ , K1 est fermé et K2 est ouvert : uC= u1=E. - pour t appartenant à [½T ; T[ , K1 est ouvert et K2 est fermé : uC= -u2=-E. La valeur moyenne est donc nulle. <uC> =0. Déterminer par un calcul d'aires, la valeur efficace Uc de la tension uC. UC=E. Avec quel appareil pourrait-on mesurer la valeur moyenne et la valeur efficace de uC ? Préciser le branchement de l'appareil de mesure et la position du commutateur AC/DC pour chacune des mesures. Un voltmètre numérique ( touche AC sélectionée), monté en dérivation aux bornes de la charge, permet de mesurer la valeur efficace. La touche DC sera sélectionnée pour mesurer la valeur moyenne. Moteur asynchrone triphasée tétrapolaire. La locomotive, équipée de ce type de moteur, est a m^me de tirer un convoi de 16 voitures. La vitesse maximale est alors de 220 km/h. Les conditions de fonctionnement d'un moteur sont les suivantes : Tension entre phases : U=2070 V ; intensité nominale du courant en ligne I= 500 A ; facteur de puissance nominale : cos j=0,89 ; puissance mécanique utile nominale Pm=1530 kW ; fréquence des tensions d'alimentation f = 140 Hz ; fréquence de rotation nominale : n=4160 tr/min. Valculer le moment TuN du couple utile nominal dans les conditions définies ci-dessus. pulsation w = 2pn avec n = 4160/60 =69,33 tr/s w =6,28*69,33 =435,41 rad/s. TuN =Pm/w =1,53 106 / 425,41 =3,51 103 Nm. Calculer la fréquence de synchronisme nS( en tr/min) sachant que le moteur est tétrapolaire. n~nS=60 f/p avec p = 2 paires de pôles et f = 140 Hz. nS = 60*140/2 =4200 tr/min. En déduire le glissement g du moteur. g=(nS-n/nS) =(4200-4160)/4200 =0,0095 ~ 1%. Calculer la puissance absorbée Pa par le moteur. Pa = 3½U I cos j =1,732*2070*500*0,89 =1595 kW. 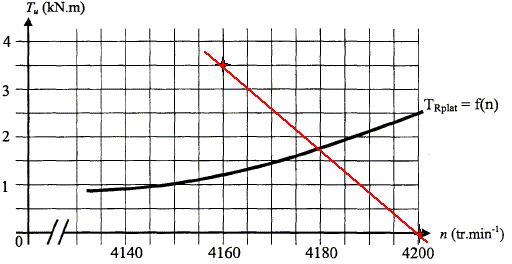Vérifier que le rendement h du moteur est environ 96 %. h = Pm/Pa =1530/1595=0,96 ou 96 %. La partie utile de la caractéristique mécanique d'un moteur asynchrone est une droite. En utilisant les valeurs nominales de fonctionnement (TuN=3,51 kNm ; n=4160 tr/min) et le point à vide (TuV=0 ; ns), tracer cette droite. La caractéristique de la charge correspond à la courbe Trplat =f(n) tracée ci-dessus. Donner la valeur de la fréquence de rotation et du moment du couple utile du moteur. Puissance et énergie. Lorsque le train remorque 16 voitures de pasagers à une vitesse de 220 km/h, la motrice développe une puissance Pm = 5,6 MW. Pour ce fonctionnement, calculer le module de la force de traction F de la motrice. Pm= F v avec Pm= 5,6 106 W et v = 220/3,6 =61,1 m/s. F= 5,6 106 /61,1 =9,16 104 N = 91,6 kN. Lors d'une phase de décélération, la motrice dispose d'un système de freinage électrique qui renvoie sur le réseau une puissance Pd=2950 kW. La phase de décélération dure Dt=30 s. Calculer l'énergie W ainsi récupérée en joule et en kWh. W= Pd Dt avec Pd =2,95 106 J W =2,95 106 *30 =8,85 107 J = 88,5 MJ. W= 2950*30/3600 = 24,6 kWh.

retour -menu