Générateur d'impulsions calibrées bac STI génie électronique 2008.  Monostable, filtre, CAN.

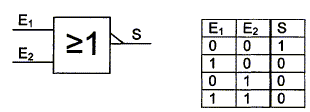
On utilise un monostable qui délivre une impulsion d'amplitude 15 V de durée 2 ms à chaque front descendant de u1. Les circuits de détection de front et de mise en forme ne sont pas étudiés. Etude du monostable. Le circuit monostable est réalisé à partir de portes NON OU de technologie CMOS, alimentées en 0V / 15 V. VL représente la tension de basculement des entrées : VL= VDD/2 = 7,5 V. 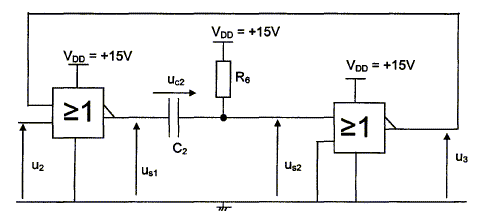On rappellela table de vérité d'une porte NON OU : Schéma structurel du monostable :   La durée de l'état instable du monostable est donnée par l'expression : T0 =0,69R6C2 avec C2 = 47 nF. Calculer la valeur de R6 de manière à avoir T0 = 2 ms. R6 = 2 10-3 / (0,69 *47 10-9) =6,17 104 W ; R6 = 61,7 kW. La tension de commande du monostable u2 est représentée ci-dessous. A l'état de repos u2 = 0 V. Déterminer la valeur de repos des tensions us2, u3, us1 et uc2. Hypothèse : u3 = 0 V. u2 = u3 = 0 : la table de vérité de la première porte NON OU conduit à uS1 = 15 V. Additivité des tensions : us1 + uc2 + uR6 = 15 ; 15 + uc2 + uR6 = 15 d'où uc2 = 0 V ; uR6 = 0 V. us1 + uc2 = us2 d'où us2 = 15 V. us2 = 15 V ; l'autre entrée de la seconde porte est à 0 V : la table de vérité de la seconde porte NON OU conduit à u3 = 0 V. A l'instant t=t0, la tension u2 passe à 15 V pendant une durée Dt très brève, D t<< 1 ms. Tracer l'évolution de la tension u3 en concordance de temps avec la tension u2 . 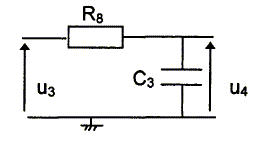Etude du filtrage. Afin d'obtenir une tension continue image de la vitesse, on filtre la tension u3 issue du monostable. Pour étudier la réponse en fréquence du filtre, on applique à son entrée une tension u3 sinusoÏdale. Aux tensions u3 et u4 on associe les nombres complexes U3 et U4. Déterminer l'expression de la fonction de transfert complexe du filtre T=U4 / U3 en fonction de R8, C3 et la pulsation w. R8 et C3 sont en série : U4= I / (jC3w) ; U3=R8 I + U4=( R8 +/ (jC3w)) I = (jR8C3w +1) / (jC3w)) I T= 1/(jR8C3w +1). Déterminer son module T. Multiplier numérateur et dénominateur par l'expression conjuguée 1-jR8Cw T =(1-jR8C3w ) / (1+(R8C3w)2) ; T = 1/ (1+(R8C3w)2)½. Calculer T pour w =0 et pour w -->oo ; en déduire la nature du filtre. T(w=0) = 1 ; T(w-->oo) = 0 ; ce filtre laisse passer les basses fréquences. Filtre passe bas. Etablir l'expression de la fréquence de coupure fc en fonction des éléments du circuit. La fréquence de coupure ( à 3 dB) est telle que : T = Tmax / 2½ ou T2 = ½ T2max avec dans ce cas Tmax= 1. T2 = 0,5 =1/ (1+(R8C3wc)2) ; 2 = 1+(R8C3wc)2 ; 1 = (R8C3wc)2 ; 1 = R8C3wc. wc = 1/(R8C3) ; or fc= wc /(2p) ; fc= 1 /(2pR8C3). On souhaite obtenir une fréquence de coupure fc= 0,1 Hz quand la résistance R8 = 330 kW. Calculer la valeur de la capacité C3 du condensateur. fc *2p R8C3= 1 ; C3= 1/(fc *2p R8) = 1/(0,1*6,28*330 103) ; C3=4,83 10-6 F.   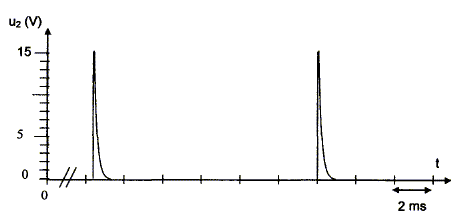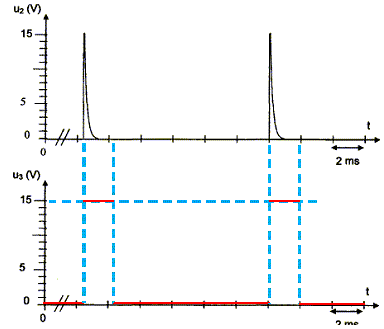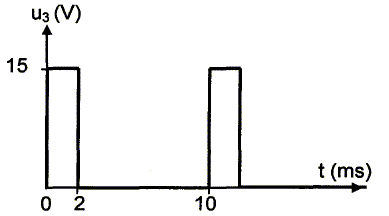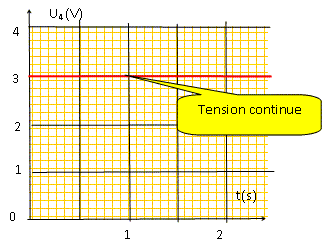On applique à l'entrée du filtre une tension u3 dont on donne l'évolution temporelle : Calculer la composante continue <U3> du signal u3.  Période T = 10 ms = 0,01 s. <U3> = (2*15 +0*8) / 10 = 30/10 ; <U3> = 3 V. Déterminer la fréquence de la composante fondamentale du spectre de ce signal. f = 1/T = 1/0,01 = 100 Hz. On suppose que le filtre ne laisse pas passer les harmoniques de la tension u3 dont la fréquence est supérieure à la fréquence de coupure fc. Représenter l'allure du spectre d'amplitude de la tension u4 en fonction de la fréquence. Toutes les fréquences supérieures à 0,1 Hz sont coupées, y compris le fondamental. Représenter l'allure du signal de sortie du filtre u4 en fonction du temps. Quel est le rôle de ce filtre ? L'affichage : La tension u4 issue du flitre dépend de la vitesse du vent v ( km/h) selon la relation : u4 = 8,21 10-3 v -2,46 10-2. La fonction mise en forme permet d'obtenir une tension u5 liée à u4 selon la relation : u5 =u4 +2,46 10-2. Exprimer la fonction u5 en fonction de la vitesse du vent. u5 = 8,21 10-3 v. Pour numériser la tension u5 on emploie un convertisseur analogique / numérique (CAN). On note N la valeur décimale du mot numérique codé en binaire naturel. On considère que l'afficheur placé à la suite du CAN indique sur 3 digits la valeur de N.( pour une vitesse de 180 km/h la valeur 180 est affichée) Exprimer la tension u5 en fonction du mot numérique N. u5 = 8,21 10-3 N. En déduire le quantum q du CAN. La résolution du CAN est donnée par la valeur du quantum " q ". La valeur de Vs va augmenter de q lorsque N va augmenter de 1. Vs = q * N d'où q = 8,21 10-3 V= 8,2 mV. Doit-on choisir un CAN à 4 bits ou à 8 bits ? Justifier. q= Du5 max / 2n avec Du5 max =8,21 10-3*180 V et q = 8,21 10-3V. Donc 2n = 180 ; n log 2 = log 180 ; n = log 180/log 2 =7,5 ; n =8 bits.

retour -menu