Pendule élastique bac S Reunion 2008.

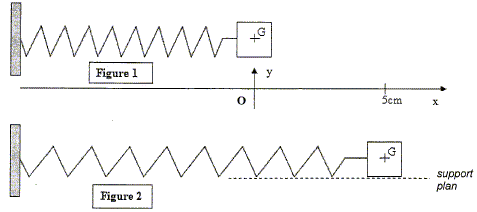
Un pendule élastique est constitué d'un ressort hélicoïdal à spires non jointives, de constante de raideur k=40 N/m, d'axe horizontal et de masse négligeable. L'une de ses extrémités est fixée à un support immobile. A l'autre extrémité est accroché un solide de masse m= 100 g pouvant osciller librement selon l'axe horizontal Ox. En position d'équilibre le centre de gravité G coïncide avec l'origine O de l'axe horizontal, orienté positivement vers la droite. 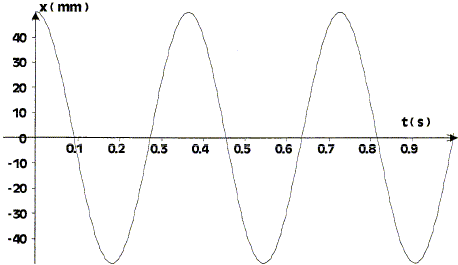Le solide est écarté de sa position d'équilibre de sorte que l'abscisse de son centre de gravité G soit +5,0 cm. A l'instant t=0, il est lâché sans vitesse initiale et son mouvement est enregistré.     Les frottements ainsi que l'amortissement du mouvement sont négligeables. g = 10 m s-2 ; on désigne par T0 la période propre des oscillations.  Faire l'inventaire des forces extérieures appliquées sur le eolide immédiatement après le lâcher et les représenter ( 1 cm pour 0,5 N). Le solide est soumis à son poids, vertical, vers le bas, valeur mg = 0,1*10 = 1 N, à l'action du support, opposée au poids et à une force de rappel exercée par le ressort, horizontale, vers la gauche, valeur T= kx0 = 40*0,05 = 2 N. L'équation différentielle du mouvement de G peut s'écrire x" + k/m x =0 où x est l'abscisse de G à la date t. Montrer que x(t) = xm cos ( 2p t/T0) est solution de l'équation différentielle du mouvement à condition d'exprimer T0 en fonction de k et m. Dériver deux fois x(t) par rapport au temps : x'(t) = -xm 2p/T0 sin(2p t/T0) ; x"(t) = -xm 4p2/T02 cos(2p t/T0) = -4p2/T02 x(t) Repport dans l'équation différentielle : -4p2/T02 x(t) +k/m x(t) = 0. -4p2/T02 +k/m =0 T02 = 4p2 m/k T0 = 2p[m/k]½. En utilisant les conditions initiales donner la valeur de xm. x(0 ) = 0,050 m ; x(0) = xm cos 0 = xm ; xm = 5,0 10-2 m. En utilisant les valeurs de m et de k, calculer la période T0. 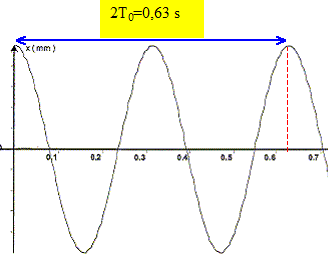m = 0,1 kg ; k= 40 N/m ; T0 = 6,28[0,1/40]½ =0,31 s. Cette valeur est-elle en accord avec celle déduite du graphique ? 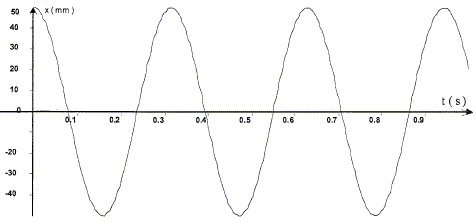Lecture graphe T0 = 0,31 s, donc accord avec le calcul. 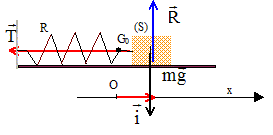Energie mécanique, vitesse : Donner l'expression de l'énergie mécanique en fonction de l'abscisse x, de la vitesse v du centre de gravité G, de la masse m et de la constante k. Nommer les deux termes qui interviennent dans cette expression. L'énergie mécanique Em est la somme de l'énergie potentielle élastique Epe= ½kx2 et de l'énergie cinétique Ec = ½mv2. Em = Epe+Ec Em = ½kx2 + ½mv2. Calculer Em à l'instant t=0. L'énergie cinétique initiale est nulle ; l'énergie mécanique est sous forme potentielle élastique. Em(0) = ½kx2m = 0,5*40*0,052 =5,0 10-2 J. En déduire la valeur de la vitesse v lors du passage à la position d'équilibre. L'énergie potentielle élastique est nulle ; l'énergie mécanique est sous forme cinétique. 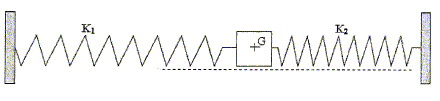De plus , en absence de frottements, l'énergie mécanique se conserve, d'où : 0,05 = ½mv2 v2 =0,05*2/m v2 = 0,1/0,1 =1 v= 1,0 m/s En travaux pratiques, un montage quelque peu différent est réalisé : sur une table à coussin d'air, on utilise deux ressorts au lieu d'un seul. L'enregistrement du mouvement est donné. On montre que ce système est équivalent à celui constitué de la même masse et d'un seul ressort de constante de raideur Kéq. L'enregistrement est réalisé avec les valeurs suivantes : k1 = 10 N/m ; k2 = 20 N/m et m = 100 g. 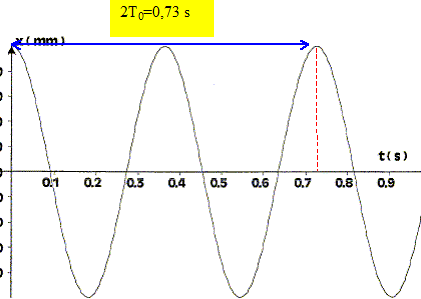Quel est l'intérêt pratique d'utiliser deux ressorts au lieu d'un ? Il est plus facile de maintenir le solide sur une droite avec deux ressorts. En utilisant le graphe ci-dessus, montrer que Kéq = k1+k2. période T0 = 0,365 s ; T0 = 2p[m/kéq]½. kéq = 4p2 m/T02 = 4*3,142*0,1/0,3652 = 29,6 kéq ~30 = k1+k2 Proposer une méthode permettant de déterminer une masse en état d'impesanteur. Mesurer la période d'un oscillateur élastique horizontal : connaissant la période et la raideur du ressort on peut en déduire la masse.

retour -menu