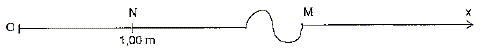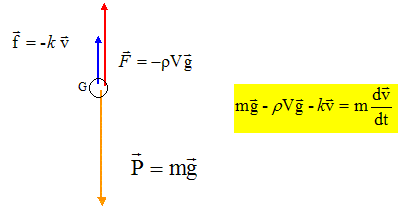Modélisations : ondes sismiques, décroissance radioactive, charge d'un condensateur, chute avec frottement

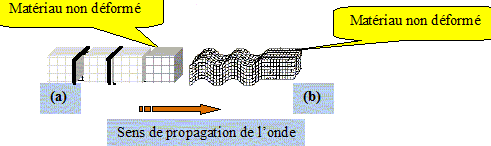
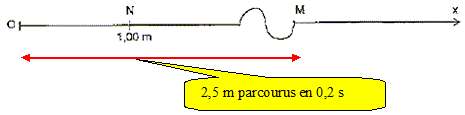
Ondes sismiques : Les séismes sont provoqués par les mouvements de plaques. Ils s'accompagnent de la propagation d'ondes à partir du foyer (lieu du séisme). Les ondes de fond se propagent à l'intérieur du globe, elles sont constituées des ondes primaires P, les plus rapides, et d'ondes secondaires S. Les ondes P sont des ondes de compression -dilatation (schéma a), les S des ondes de cisaillement vertical (schéma b).   Ces ondes mécaniques se propagent dans toutes les directions, à partir du foyer du séisme, à travers le globe terrestre : ce sont des ondes mécaniques progressives. Les ondes P sont longitudinales : alternance de compression et dilatation dans la direction de propagation de l'onde. Les ondes S sont transversales : cisaillement vertical, perpendiculaire à la direction de propagation de l'onde. On modélise la propagation des ondes S par la propagation d'une onde sur une corde tendue. Le séisme est matérialisé par une perturbation à la source O à t0 = 0 s. L'allure de la corde à la date t1 = 0,20 s est schématisée ci-dessous :   Célérité de l'onde. v = 2,5 / 0,20 =12,5 m/s ~ 13 m/s. Une modification de l'amplitude de la perturbation ne modifie la célérité de l'onde. Une modification de la tension de la corde modifie la célérité de l'onde : Plus le milieu est rigide, plus la célérité est grande. Sur une corde, la célérité d'une onde est d'autant plus grande que la corde est plus tendue. Calcule du retard t de la perturbation en un point N situé à 1,00 m de la source, par rapport à la source O. t = ON / v = 1,00 /12,5 = 0,080 s. Allure du déplacement du point N de la corde sur un axe temporel. Chaque point du milieu reproduit le mouvement de la source ( c'est à dire celui du point M qui va commencer par descendre ) avec un certain retard. On modélise toujours la propagation des ondes S par la propagation d'une onde sur une corde tendue, mais le séisme est matérialisé par un vibreur de fréquence f = 100 Hz. Calcul de la période et de la longueur d'onde. T = 1/f = 1/100 =1,00 10-2 s. l = v / f = 12,5/ 100 =0,125 m ~ 0,13 m. Modélisation de la décroissance radioactive. 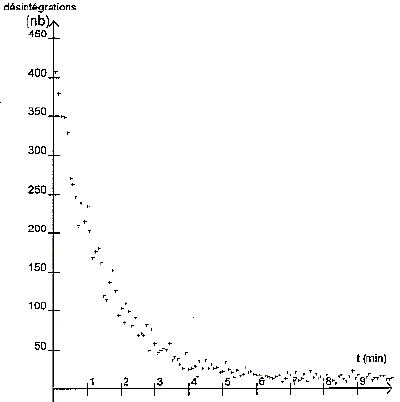L'étude expérimentale porte sur le radon 220 noyau radioactif émetteur a. À l'aide d'un compteur de radioactivité naturelle, on effectue une acquisition toutes les 5 s pendant 10 min. Chaque acquisition a une durée de 1 s. On obtient la courbesuivante, représentant le nombre de désintégrations détectées en fonction du temps. On donne 22086Rn ; 21684Po. 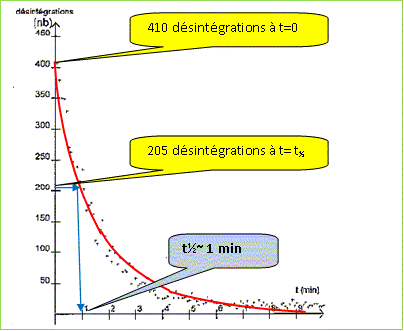Composition du noyau du radon 220. 86 protons et 220-86 = 134 neutrons. Equation de désintégration du radon 220 en polonium 216. 22086Rn --> 21684Po +42He. Détermination graphique de la demi-vie t½ du radon 220. La méthode utilisée doit être clairement explicitée sur le graphique. 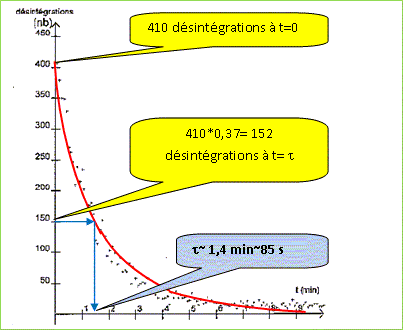Détermination graphique de la constante de temps t. En déduire la constante radioactive l.   l = 1/t =1/85 =0,0117 ~ 0,012 s-1. Le logiciel modélise le phénomène par la fonction n(t) = 450.e-0,012.t avec t en s. Valeur de la constante radioactive l. 0,012 s-1. Relation l = ln2 / t½. d'une part : n(t) = n0.e-l.t ; d'autre part à t=t½ , n(t½) = ½ n0 = n0.e-l.t½ ; d'où ½ = e-l.t½ ; ln ½ = -l.t½ ; ln2 =l.t½ ; l = ln2 / t½ ln2 / t½ =ln2 / 60 =0,0115 s-1, valeur très proche de la valeur de l ( 0,0117 s-1). Définition de l'activité et son unité. Nombre de désintégrations par seconde ; l'activité s'exprime en becquerel ( Bq). 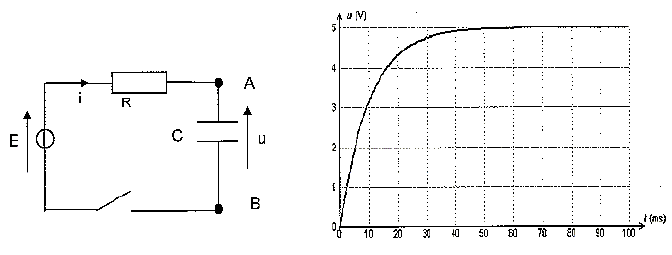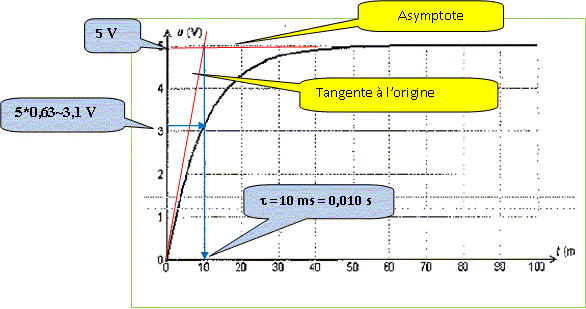Charge d'un condensateur. On charge un condensateur, initialement déchargé, sous une tension continue E. On réalise l'acquisition par ordinateur de la tension u aux bornes du condensateur. Données : C = 10 mF ; R = 1,0 kW . Relation entre la charge du condensateur q(t) = qA(t) et l'intensité du courant i(t). i(t) = dqA(t) /dt. Relation entre q(t), la tension u(t) aux bornes du condensateur et sa capacité C. q(t) = C u(t). Montrons que la tension u(t) vérifie l'équation différentielle suivante : E = R.C. du/dt + u. Additivité des tensions : E = Ri + u ; or i = dq/dt et q= Cu avec C une constante d'où i = Cdu/dt. par suite E= RCdu/dt + u. La solution proposée par le logiciel de modélisation est : u = 5,0.(1 - e-100.t) avec t en s. A quoi correspondent les valeurs numériques 5,0 et 100 ? La tension aux bornes du condensateur chargé vaut 5,0 V ; 100 ( en s-1) est l'inverse de la constante de temps du circuit : 100 = 1/(RC). Détermination graphique de la constante de temps t sur la courbe fournie en annexe. Calculer sa valeur théorique et conclure. Valeur théorique t = RC = 103*10 10-6 = 10 10-2 s, en accord avec la valeur expérimentale. Chute avec frottement. 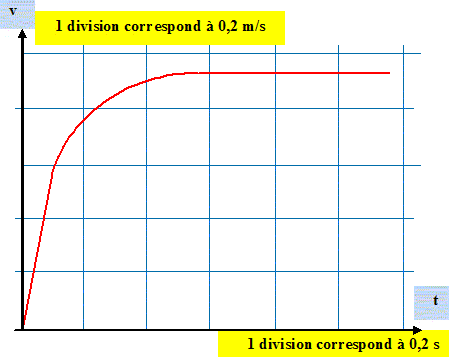On étudie la chute d'une bille en acier dans un fluide. On se place dans le référentiel du laboratoire et on prend un axe vertical Oz dirigé vers le bas. L'acquisition de la vidéo permet au logiciel de déterminer l'évolution des valeurs de la vitesse de la bille en fonction du temps. Bille : rayon R = 1,00 cm ; volume : V= 4,20 cm3 ; masse m = 32,6 g. On prendra g = 9,81 m s-2. Fluide : viscosité : h=1,50 Ns m-2 ; masse volumique r = 1,3 103 kg m-3. On prend comme modèle pour la force de frottement f = kv avec k = 6.p .R.h et v vitesse de la bille. La poussée d'Archimède a pour expression F = r Vg. Représentation, sur un schéma, les forces extérieures appliquées à la bille en chute verticale dans le fluide. 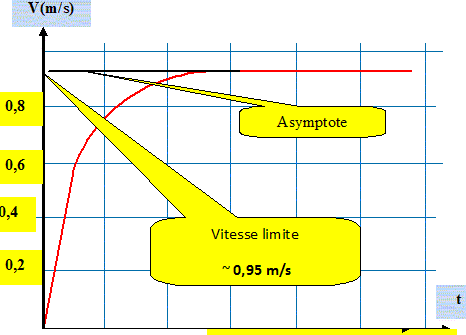En appliquant la deuxième loi de Newton, montronsr que l'expression de l'équation différentielle régissant l'évolution de v est de la forme a - b.v = dv/dt avec a = 8,2 m.s-2 et b = 8,7 s-1. Ecrire la seconde loi de Newton projétée sur l'axe Oz, vertical orienté vers le bas : mg-rVg-kv=mdv/dt. Diviser par m chaque terme : g-rVg/ m-k/ m v=dv/dt. On pose a = g(1-rV/ m) et b = k/ m. Détermination de la vitesse limite à l'aide du graphique. Calcul de la vitesse limite à l'aide de l'équation différentielle et conclure. Lorsque la vitesse limite est atteinte, le mouvement est rectiligne uniforme ( valeur de la vitesse constante : dvlimite / dt = 0) ; alors l'équation différentielle s'écrit : a - bvlimite = 0 ; vlimite =a/b = 8,2 / 8,7 ~ 0,94 m/s, en accord avec la valeur expérimentale. Modélisation et longitude. " Le système GALILEO sera constitué de satellites en orbite autour de la Terre. Ils envoient des ondes électromagnétiques vers la Terre, ce qui permet de déterminer la longitude, la latitude et l'altitude. Avec ce système de radionavigation, chacun pourra connaître sa position à un instant donné. Le modèle de calcul repose sur une triangulation avec au moins 4 satellites et une synchronisation sur les horloges atomiques embarquées sur les satellites (horloges au césium ou rubidium avec une précision de 10 -12 s). Célérité de la lumière c = 3,00.108 m.s-1 " D'après le site futura-sciences.com Avec un modèle d'orbite circulaire, la vitesse du satellite situé à l'altitude h = 2,00.104 km s'exprime par la relation v =[GM/(R+h)]½ avec : G = 6,67.10 -11 SI : constante de gravitation ; R = 6380 km : rayon de la Terre ; M = 5,98.1024 kg : masse de la Terre. Calcul de la vitesse du satellite, en déduire sa période. R = 6,38 106 m ; h = 2,00.107 m ; R+h =2,638 107 m ; v = [ 6,67.10 -11 *5,98.1024 /2,638 107]½ =3,888 103 m/s ~ 3,89 103 m/s. Circonférence de l'orbite : 2p (R+h) =2*3,14*2,638 107 =1,657 108 m. Période = circonférence de l'orbite / vitesse =1,657 108 / 3,888 103 =4,26 104 s. Détermination de la durée t minimale mise par les ondes envoyées par le satellite pour arriver au récepteur situé au sol. Dans le cas d'un récepteur situé à la verticale du satellite : t = (R+h)/c =2,638 107 / 3 108 =8,79 10-2 s. Le système GALILEO prévoit un écart sur la position d'un centimètre. Quel sera l'écart Dt sur la durée t ? La " précision " des horloges est-elle suffisante ? 1 cm = 0,01 m ; Dt = 0,01 / 3 108~ 3 10-11 s, valeur supérieure à la précision des horloges. Les horloges sont donc assez précises. Les horloges atomiques au césium fonctionnent sur une transition atomique de fréquence n =9 192 631 770 Hz, calculer l'énergie du photon correspondant. La constante de Planck a pour valeur h = 6,63.10 -34 J.s E = h n ; E = 6,63.10 -34 *9 192 631 770 =6,09 10-24 J.

retour -menu