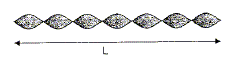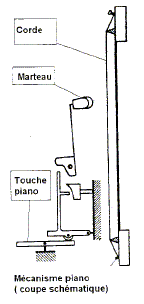
Etude d'un piano bac S Liban 2008.

Le piano est un instrument dont les cordes de longueur L, sont mises en vibration par le choc des marteaux. Chaque marteau est actionné en appuyant sur une touche du piano. Pour le piano étudié, la tension des différentes cordes est à peu près la même pour toutes. Chaque corde est frappée au septième ou au neuvième de sa longueur de façon à éliminer les harmoniques 7 ou 9 les plus défavorables à la qualité du son émis. On donne l'expression de la célérité du son dans une corde : v=[F/m]½. V : célérité en m/s F: tension de la corde (N) m : masse linéique de la corde (kg m-1) Représenter sur un schéma une corde de longueur L, fixée à ses deux extrémités, vibrant dans le mode fondamental. Préciser la position des noeuds et des ventres de vibration.   Donner la relation entre la longueur L de la corde et la longueur d'onde l pour le mode fondamental. L =½ l. En déduire l'expression littérale de la fréquence fondamentale f1 en fonction de la célérité et de la longueur de la corde. f1 = c/l et l = 2L d'où : f1 = c / (2L). La corde du piano correspondant au la3 émet un son complexe de fréquence égale à 440 Hz. A quelle caractéristique d'un son est associée la fréquence d'une note ? A la hauteur du son. Quelle est la fréquence associée au mode fondamental de vibration de la corde ? La fréquence du son complexe correspond à la fréquence fondamentale : ici f1 = 440 Hz.   On donne ci-dessous le schéma d'une corde vibrant dans le mode 7.   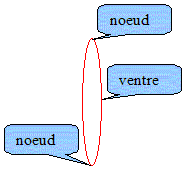Donner la fréquence de l'harmonique de rang 7. f7 = 7 f1 = 7*440 = 3080 Hz= 3,08 kHz. Pourquoi un marteau frappant au septième de la longueur de la corde élimine t-il l'harmonique de rang 7 de l'instrument ? Le marteau frappe sur un noeud de vibration ( point de la corde qui ne vibre pas). Quelle caractéristique du son émis par l'instrument est modifiée par la suppression de l'harmonique de rang 7 ? Le timbre du son est modifié. On considère un clavier de piano comportant sept octaves. Si toutes les cordes avait même masse linéique et étaient soumises à la même tension, leur longueur devrait être comprise entre 6 cm et 8 m. La corde de 8 m de longueur correspondrait-elle à la note la plus grave ou à la plus aigue ? Justifier. v=[F/m]½ et f = v/(2L). f = [F/m]½/ (2L) = Constante / L. la fréquence est d'autant plus petite que la longueur de la corde est plus grande. Un fréquence plus faible correspond à un son plus grave. Pour éviter des longueurs aussi importantes, on utilise des cordes filiées. Autour d'un fil d'acier, toujours soumis à la même tension, on enroule en spires serrées un fil de cuivre soudé aux deux extrémités du fil d'acier. Les différentes cordes filiées, toutes de même longueur, peuvent atteindre un diamètre de l'ordre du centimètre. Quelle caractéristique de la corde est modifiée par l'enroulement du fil de cuivre sur le fil d'acier ? La masse de la corde filiée augmente avec l'épaisseur du fil de cuivre ; la longueur de la corde reste constante : donc la masse linéique m de la corde varie. La note de fréquence f=27,5 Hz est obtenue pour une corde filiée. La longueur de celle-ci est L= 0,50 m. La tension de la corde est F= 400 N. Calculer la masse de la corde. v=[F/m]½ et f = v/(2L). m = F/v2 = F/(2f L)2 = 400 /(27,5)2 =0,529 kg m-1. Masse de la corde m = m L = 0,529*0,50 = 0,26 kg.

retour -menu