Quelques propriétés de la flûte de Pan bac S Inde 2008. lycée-francais-pondichery

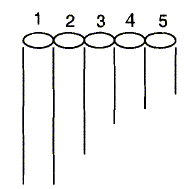
La flûte de Pan est très certainement un des instruments les plus faciles à fabriquer. Il suffit de quelques bouts de roseau bien évidés, d'un peu de bougie et d'un bon couteau ! Cette flûte consiste en une série de tuyaux de longueurs différentes qui sont maintenus ensemble par des ligatures (voir figure ci-dessous). Une extrémité de chaque tuyau est à l'air libre, l'autre (le fond) est fermée Une fois construite, cette flûte doit jouer les notes do3 , mi3 , sol3 , do4 et mi4. Les deux dernières notes sont à l'octave respectivement des notes do3 et mi3, c'est-à- dire qu'il y a une octave entre do3 et do4 (idem pour mi3 et mi4), la note do4 étant plus aiguë que do3 (idem pour mi4 plus aiguë que mi3). Une recherche documentaire a permis de connaître les fréquences des trois premières notes : notes do3 mi3 sol3 Fréquence en Hz 262 328 393 Rappeler la définition de deux sons à l'octave et déterminer les fréquences des deux notes do4 et mi4. Les fréquences de 2 notes séparées d'une octave sont telles que : f(do4) = 2* f(do3) = 2*262 = 524 Hz. f(mi4) = 2* f(mi3) = 2*328 = 656 Hz. On rappelle que : - les sons sont produits par les vibrations des colonnes d'air contenues dans les tuyaux ; - la vitesse de propagation (célérité) des sons dans l'air est c = 340 m/s. Une étude plus fine montre qu'il y a toujours un nœud de vibration à une extrémité fermée d'un tuyau et un ventre de vibration à une extrémité ouverte. Définir ce qu'on appelle nœud de vibration et ventre de vibration. A un noeud de vibration l'air ne vibre pas ( amplitude nulle) A un ventre de vibration, l'air vibre avec une amplitude maximale. Dans quel type d'ondes peut-on observer des nœuds et des ventres de vibration ? Ondes dites "stationnaires" On note l la longueur d'onde du son de fréquence f. On rappelle qu'un nœud et un ventre consécutifs sont distants de 0,25 l . Exprimer l en fonction de f et des données du problème. l = c /f avec c (m/s) : célérité du son dans l'air. Montrer que le tuyau de la flûte de longueur L est accordé sur le son de longueur d'onde l si L = n ½ l + 0,25 l , n étant un nombre entier positif ou nul. D'une part deux ventres de vibration consécutifs ( ou deux noeuds consécutifs) sont distants de ½l. D'autre part une extrémité du tuyau est ouverte et l'autre est fermée, d'où :   par suite : L = n ½ l + 0,25 l avec n entier ou nul. On appelle mode chaque valeur de n. 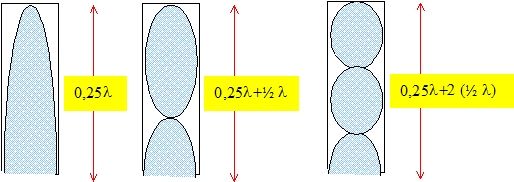Qu'appelle-t-on mode fondamental ? Que vaut L dans ce cas ? Le mode fondamental correspond à n=0, c'est à dire la plus petite valeur de n ; la longueur L vaut 0,25 l.   Déterminer la longueur de chacun des 5 tuyaux de la flûte de Pan dont le fondamental est accordé sur chacune des 5 notes do3 , mi3 , sol3 , do4 et mi4. note do3 mi3 sol3 do4 mi4 fréquence f Hz 262 328 393 524 656 l(m) = c/f = 340/f 340/262=1,298 1,036 0,865 0,6488 0,5183 L= 0,25l(m) 0,324 0,259 0,216 0,162 0,130 On dit parfois que les seuls sons possibles pour une flûte de Pan sont les harmoniques impairs. Justifier cette affirmation. 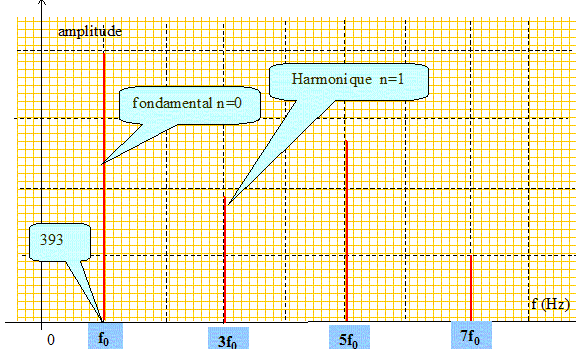L = 2n *0,25 l + 0,25 l   =( 2n+1)*0,25 l. Or l = c/f d'où : L = ( 2n+1)*0,25 c/fn soit fn =( 2n+1)*0,25 c/L. De plus pour n=0, on trouve la fréquence f0 du fondamental : f0 =0,25 c/L. Par suite : fn =( 2n+1)f0 : les fréquences de harmoniques sont des multiples impairs de la fréquence du fondamental. Un microphone enregistre le son produit par le tuyau n°3. La tension-image de ce son est ensuite analysée par un ordinateur. Représenter ce que donnerait une analyse fréquentielle (ou spectre fréquentiel) du son produit par le tuyau n°3 : en abscisses les fréquences des modes et en ordonnées les amplitudes (arbitraires). Votre schéma devra comporter au moins 4 harmoniques.       La célérité du son dans l'air augmente (faiblement) avec la température. Prévoir qualitativement si les notes jouées vont être toutes légèrement plus aiguës ou plus graves quand la température augmente. On ne raisonnera que sur le mode fondamental de vibration et on négligera la dilatation des tuyaux. f0 =0,25 c/L.   La longueur d'un tuyau étant constante, si la célérité augmente légerement, alors la fréquence croît un petit peu. A une fréquence plus élevée correspond un son plus aigu. Il en est de même pour chaque tuyau.

retour -menu