Michael Faraday : électrolyse, bobine inductive bac S Asie 2008.

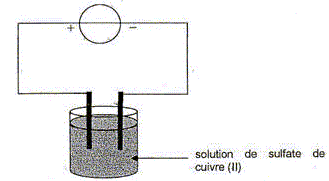
Electrolyse du sulfate de cuivre. On réalise l'électrolyse du sulfate de cuivre (Cu2+aq + SO42-aq) entre deux électrodes inataquable de carbone afin d'obtenir à l'une des électrodes un dépôt de cuivre. Ecrire l'équation de la réaction à l'électrode où se produit le dépôt de cuivre. S'agit-il d'une oxydation ou d'une réduction ? Réduction des ions cuivre II : Cu2+aq + 2e- = Cu(s). Préciser le nom de l'électrode où se produit ce dépôt ainsi que le signe + ou - de la borne du générateur auquel elle est reliée. Cathode reliée à la borne négative du générateur. Donner une relation entre la quantité de matière de cuivre déposée nCu au bout d'une durée Dt d'électrolyse et la quantité d'électrons (mol) ne ayant circulé dans le circuit ? D'après les nombres stoechiométriques de l'équation ci-dessus :  ne = 2 nCu.   Exprimer la quantité d'électrons (mol) ne en fonction de l'intensité I du courant d'électrolyse, la durée Dt de l'électrolyse, le nombre d'Avogadro NA et la charge élémentaire e. Quantité d'électricité : Q = I Dt. Q( coulomb) ; I ( ampère) ; D t ( seconde) Valeur absolue de la charge d'une mole d'électron : 1 Faraday = NA e. Valeur absolue de la charge de ne mole d'électron : Q =NA e ne. ne =I Dt / (NA e) Etablir la relation entre la quantité de matière de cuivre déposé nCu au bout de Dt et l'intensité I du courant et montrer que la quantité de matière de cuivre est proportionnelle à l'intensité du courant. D'une part : ne =I Dt / (NA e) D'autre part :  ne = 2 nCu. Par suite : nCu =I Dt / (2NA e). k=Dt / (2NA e) étant constant, nCu = kI, avec k constante de proportionnalité. Exprimer la masse de cuivre mCu déposée au bout de Dt et montrer que la masse de dépôt est proportionnelle à la masse molaire de l'élément déposé, divisée par un petit nombre entier. Que vaut ce petit nombre entier ? mCu = nCu M(Cu). mCu = k I M(Cu) = I Dt / (2NA e) M(Cu). On pose : n =2NA e/ (I Dt) d'où : mCu =M(Cu)/n. Lorsque I Dt est égal à 1 Faraday, NA e/ (I Dt) vaut 1 et n = 2. Bobine inductive.  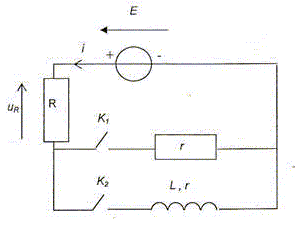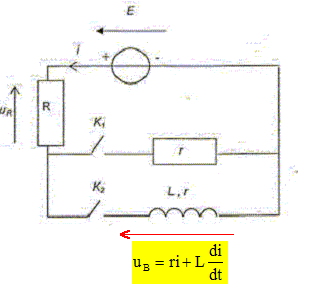On réalise le montage suivant constitué d'un générateur de tension constante de valeur E=3,0 V, de deux interrupteurs K1 et K2, d'un conducteur ohmique de résistance R=90 W, d'un second conducteur ohmique de résistance r, d'une bobine de résistance r ( identique à celle du second conducteur ohmique )et d'inductance L. Une interface reliée à un ordinateur permet de saisir les valeurs instantannées de la tension uR. Deux saisies sont successivement réalisées. 1ère saisie : K2 reste ouvert, on ferme K1. 2ème saisie : K1 reste ouvert, on ferme K2. On programme la feuille de calcul afin d'obtenir dans les deux cas l'évolution de l'intensité i du courant en fonction du temps. 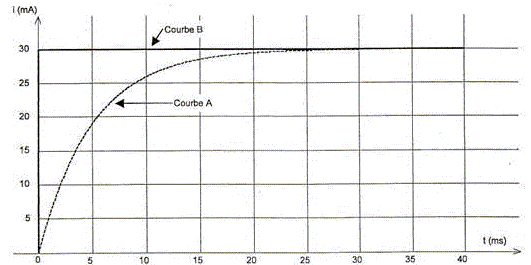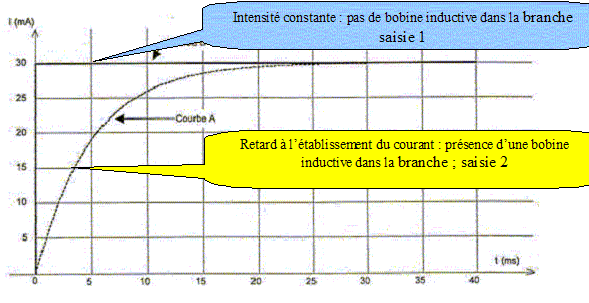Quelle relation faut-il programmer pour obtenir i, intensité du courant en fonction du temps ? L'intensité qui travers un résistor et la tension à ses bornes sont proportionnelles. i= uR/R.  Attribuer à chaque saisie la courbe correspondante en justifiant.   Représenter sur le circuit la flèche symbolysant la tension uB aux bornes de la bobine. Donner l'expression littérale de la tension uB en fonction de r, L et i. 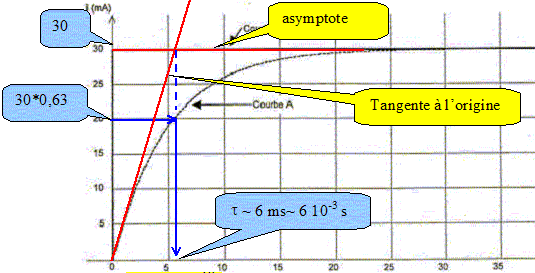Etude de la seconde saisie. Etablir l'équation différentielle qui régit l'évolution de l'intensité i quand on ferme l'interrupteur K2. additivité des tensions : E=uR+uB. E = Ri +ri+Ldi/dt ; di/dt + (R+r)/L i = E/L. En déduire l'expression littérale de l'intensité I en régime permanent. Déterminer graphiquement sa valeur puis calculer r. En régime permanent l'intensité est constante : dI/dt = 0; par suite E = RI +rI I =E/(R+r) =0,030 A r = E/I-R =3/0,03-90 = 10W Inductance de la bobine. Donner l'expression littérale de la constante de temps t. Par analyse dimensionelle vérifier que t est homogène à un temps. t=L/(R+r) énergie = ½L i2 ; L est une énergie divisée par une intensité au carré : L s'exprime en J A-2. énergie ( effet Joule) = Ri2t ; R est une énergie divisée par un temps et par une intensité au carré. R s'exprime en J A-2 s-1. Par suite L/ R s'exprime en seconde : t est homogène à un temps. Déterminer graphiquement t.     En déduire l'inductance L de la bobine. L= t (R+r) 6 10-3*100 L=0,6 H Justifier la limite commune aux deux saisies. 1er point : en régime permanent, la bobine se comporte comme un résistor de résistance r. 2éme point : les deux branches ont la même résistance électrique.

retour -menu