Alimentation simplifiée d'un injecteur d'automobile bac S Antilles 09/08.

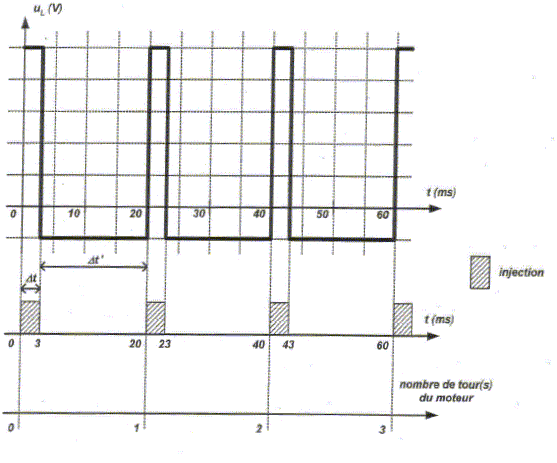
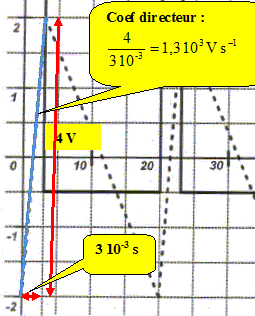
Dans les moteurs d'automobiles modernes le carburant est introduit à l'aide d'injecteurs. L'ouverture et la fermeture de l'injecteur sont commandées par un électroaimant. Dans cet exercice on s'intéresse à la bobine composant l'électroaimant. Le document ci-dessous représente l'évolution de la tension uL(t) aux bornes de l'électroaimant et la périodicité de l'injection lorsque le moteur fonctionne à 3000 tous par minute. 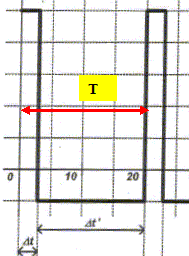Etude de la tension aux bornes de la bobine. Déterminer la période T de la tension uL(t). T = Dt + Dt' = 20 ms = 2,0 10-2 s. La période T' du cycle d'injection vaut-elle Dt, D t' ou D t+Dt' ? Comparer T et T'. La durée de l'injection est Dt= 3 ms ; une nouvelle injection se produit Dt'= 17 ms   après la fin de l'injection précédente. T' = Dt+ Dt'= 20 ms = T. Montrer que la valeur de T' est en accord avec les "3000 tours/min" effectués par le moteur. nombre de tours par seconde = 3000 60 = 50 tr s-1. Une injection se produit à chaque tour : donc il y a 50 injections par seconde. T ' = 1 50 = 2,0 10-2 s. 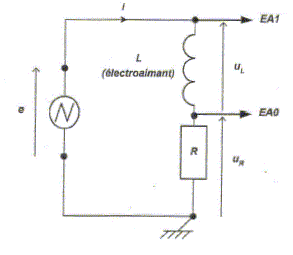Détermination de l'inductance L de la bobine de l'injecteur. 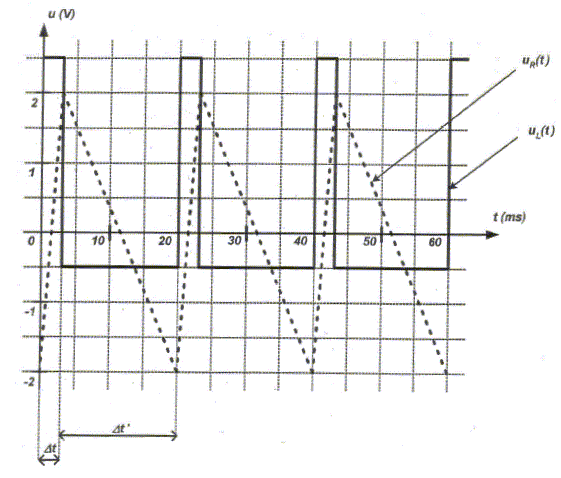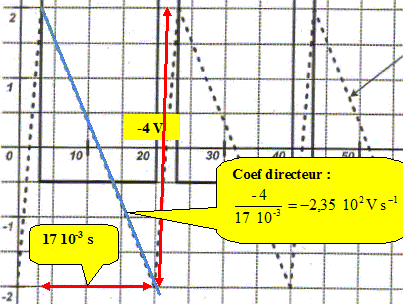Pour cela on réalise le circuit suivant : Le générateur utilisé délivre une tension triangulaire asymétrique. La résistance R vaut 1,00 kW. Le système d'acquisition et de traitement permettent d'obtenir les courbes suivantes :   Quelle tension visualise t-on sur l'entrée EA0 ? uR(t). Quelle tension visualise t-on sur l'entrée EA1 ? uR(t) + uL(t) = e(t). Comment a t-on obtenu uL(t) à partir des tensions enregistrées en EA0 et EA1 ? uL(t) = e(t) -uR(t). Soustraire la tension visualisée sur EA0 à la tension visualisée sur EA1. Donner l'expression littérales de uR(t) en fonction de i(t). En déduire l'expression de di(t) / dt. uR(t) = R i(t) ; R est une constante. duR(t) di(t) = R dt dt di(t) dt = 1 R . duR(t) dt Compléter le tableau suivant. Dt Dt' duR(t) dt V s-1 1,3 103 ............. di(t) dt ............. 1,3 ............. uL(t) V ............. ............. L ............. ............. ............. 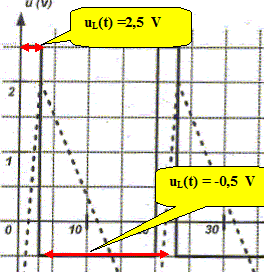et Dt Dt' duR(t) dt V s-1 1,3 103 -2,4 102 di(t) dt A s-1 1,3 -0,24 uL(t) V 2,5 -0,5 L H 1,9 2,1    En déduire la valeur de l'inductance L. uL(t) = L . di(t) dt ; L =uL(t) dt di(t) sur [0 ; 3 ms] : L = 2,5 1,3 = 1,9 H sur ]3 ; 20 ms] : L = -0,5 -0,235 = 2,1 H Le constructeur indique L ~ 2 H. Commenter les valeurs obtenues.  Ecart relatif : 0,1/2 *100 = 5 % A 5 % près les valeurs trouvées sont en accord avec l'indication du constructeur ; de plus ce dernier fournit une valeur indicative, approchée, de l'inductance.

retour -menu