enseignement ; concours CAPLP externe 2006 : angle de raccordement d'un liquide sur une surface plane, par une méthode optique

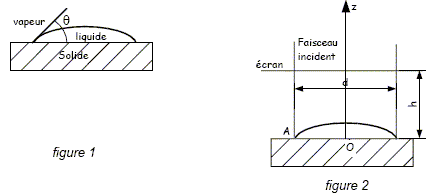
Lorsqu'un liquide est déposé sur une surface plane horizontale, il forme généralement une goutte ou, si son volume est important, une flaque.

La ligne où se coupent les trois interfaces solide/liquide, liquide/vapeur et vapeur/solide est appelée ligne triple. Pour une goutte ayant la symétrie de révolution, cette ligne triple est un cercle de rayon r.

En un point de la ligne triple, l'interface liquide/vapeur fait avec le plan solide un angle q, appelé angle de contact ou de raccordement (figure 1) . On s’intéresse aux liquides pour lesquels q varie entre 0 et 45°.

On envisage le dispositif représenté sur la figure 2, dans laquelle les proportions ne sont pas respectées.

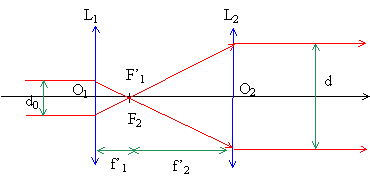
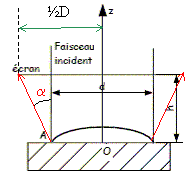
Une goutte de liquide ayant la symétrie de révolution autour de l'axe Oz est posée sur le plan solide, d’équation z = 0. Elle est éclairée par un faisceau laser élargi, d'axe Oz et de section circulaire de diamètre d = 5 mm (d = 2r). La trace du faisceau réfléchi par la goutte de liquide sur un écran semitransparent confondu avec le plan d'équation z = h est un disque dont le bord est un cercle d'axe Oz et de diamètre D > d.

Le faisceau cylindrique issu du laser possède un diamètre d₀ = 1 mm. Schématisons un montage permettant d'en faire un faisceau élargi de diamètre d = 5 mm à l'aide d'une lentille mince convergente, de distance focale f'₁, suivie d'une lentille mince convergente, coaxiale à la précédente, de distance focale f'₂.

Calcul de f'₂ et la distance L entre les deux lentilles pour f'₁ = 1 cm.

f'₂ = f'₁ d/d₀ = 1*5/1 = 5 cm ; L=O₁O₂ = f'₁ +f'_{2 = 6 cm.}

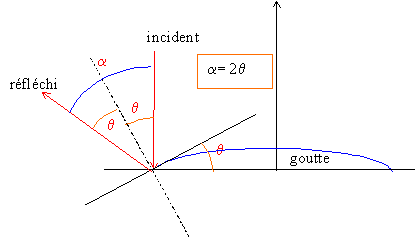
Le plan tangent à l'interface liquide/vapeur en A fait avec le plan d’équation z = 0 un angle q.

Déduction de l'angle que fait le rayon lumineux réfléchi par l'interface liquide/vapeur avec Oz.

Soit un rayon lumineux frappant la goutte ailleurs que sur la ligne triple et q₁ l'angle que fait

le plan tangent à l'interface liquide/vapeur en ce point avec le plan d’équation z = 0.

si q₁ <q alors a₁ <a : les rayons se réfléchissant sur la goutte ailleurs que sur la ligne triple ne contribuent pas à la délimitation de la tache observée.

Diamètre D de la tache observée en fonction de q, d et h :

½D = ½d + h tan a = ½d + h tan (2q) ; D = d + 2h tan (2q) ;

Calcul de l'angle de contact q pour une goutte d'eau posée sur du verre traité sachant que d = 5 mm, h = 12 cm et D = 4,2 cm.

tan (2q) = ½(D-d) /h = 0,5(4,2-0,5) / 12 = 0,154 ; 2q =0,153 rad ; q = 7,6 10^-2 rad.