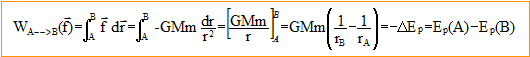|
enseignement ; concours CAPLP externe 2006 : gravitation et satellite |
|||
|
|||
|
Loi de la gravitation universelle ( Newton est à l'origine de cette loi ) Deux corps A et B de masses respectives mA et mB séparés d'une distance d=AB exercent l'un sur l'autre des forces opposées attractives, importantes dans l'infiniment grand, négligeables dans l'infiniment petit.
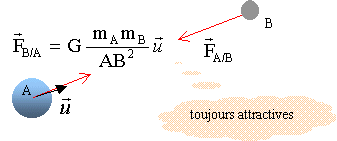
Les trois autres interactions fondamentales de la Physique sont l'interaction électromagnétique, l'interaction forte, l'interaction faible. L'interaction
électromagnétique et l'interaction
forte
existent à
l’échelle d’un noyau atomique.
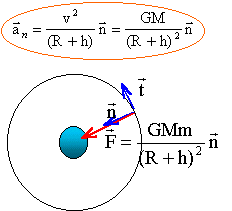
Le satellite de masse m, assimilable à un point matériel, est en orbite circulaire autour de la Terre à une altitude h. On suppose que la Terre, de rayon R et de masse M, a une répartition de masse à symétrie sphérique. Référentiel géocentrique : Le référentiel géocentrique a pour origine le centre de la Terre et des axes parallèles à ceux du référentiel héliocentrique. Ce référentiel peut être considéré comme galiléen pour des durées de quelques minutes. Montrons que la trajectoire circulaire implique un mouvement uniforme : Le satellite n'est soumis qu'à la force de gravitation centripète ; cette force est à chaque instant perpendiculaire à la vitesse et en conséquence sa puissance est nulle. L'énergie cinétique du satellite ne varie pas : donc la valeur de la vitesse est constante ( mouvement uniforme). Expression de la vitesse v et la période T de ce satellite en fonction de G, M, R, h : le satellite est soumis à la seule force de gravitation centripète exercée par la planète
M : masse (kg) de la planète ; m : masse du satellite (kg) ; R (m) rayon planète ; h (m) altitude depuis le sol suivant l'axe n la seconde loi de Newton s'écrit : GMm /(R+h)² = m aN= mv²/ (R+h) d'où la valeur de la vitesse (m/s):
v² =GM / (R+h).
indépendante de la masse du satellite
La période de révolution T du satellite (seconde) est le temps mis par le satellite pour faire un tour et ce d'un mouvement uniforme. 2 p (R+h) =vT élever au carré, puis remplacer v² par l'expression ci dessus. 4p² (R+h) ² = v² T² = GM/ (R+h) T² ou T² =4p² /(GM)(R+h)3. soit T² /(R+h)3 = 4p² / (GM) rapport constant pour une planète donnée.(3ème loi de Kepler) distance en mètre, période en seconde, masse en kg. T2 =4p2(R+h)3/(GM) avec R= 6,38 106 m ; h= 8,32 105 m ; G= 6,67 10-11 m3 kg-1 s-2 ; M=5,98 1024 kg. T2 = 4*3,142*(6,38 106+8,32 105)3 / (6,67 10-11*5,98 1024) =3,71 107 s2 ; T= 6,09 103 s Cette valeur étant différente du jour sidéral Tj=86164s, SPOT n'est pas géostationnaire Pour « établir » cette loi, Képler s’appuya sur les observations faites par une autre personne : Tycho Brahé.
Les vecteurs sont écrits en bleu et en gras. La force exercée par la Terre sur le satellite en orbite circulaire est une force centrale qui dérive d’une énergie potentielle Ep, ainsi on a : F = -dEp/dr er où er représente le vecteur unitaire radial et r le rayon de l'orbite ciculaire. Expression de l’énergie potentielle Ep du satellite en fonction de G, M, m et r (on adoptera comme origine de l’énergie potentielle celle pour r infini). Expression vectorielle du champ de force f(r) auquel est soumis le satellite : Le satellite n'est soumis qu'à la force de gravitation attractive exercée par la Terre. La direction de cette force passe toujours par le point O, centre de la Terre : il s'agit donc d'un champ de forces centrales. f(r) = GMm/r2(-er) Montrons que la force f qui s'exerce sur le satellite S dérive d'une énergie potentielle de gravitation Ep. Le travail de la force f(r) ne dépend que des positions initiale et finale ( peu importe le chemin suivi) : la force est conservative. On peut associer à cette force, une fonction scalaire ou énergie potentielle notée Ep(r), définie à une constante près ; la variation de l'énergie potentielle entre les points A et B est égale à l'opposée du travail de la forcef(r) entre ces points.
En prenant B situé à l'infini ( par convention cette énergie potentielle est nulle à l'infini), il vient : Ep = -GMm/r. Pour éloigner deux masses l'une de l'autre, il faut exercer un travail moteur, opposé au travail de la force de gravitation donc égal à la variation d'énergie potentielle : DEp >0 ; Ep fin - Ep initial >0 ; or Ep fin tend vers zéro donc Ep initial <0 l'énergie potentielle de gravitation est donc négative quelle que soit la distance r finie Le signe négatif dans le terme d'énergie potentielle traduit le fait que celle-ci augmente si R croît. Expression de la vitesse d’évasion (vitesse de libération) du satellite pour laquelle l’énergie mécanique E s’annule. Expression de l'énergie mécanique Esol de ce satellite dans le référentiel géocentrique avant son lancement : l'énergie potentielle vaut Ep= -GMm/R ; l'énergie cinétique communiquée par la Terre vaut : Ec = ½mv2 avec v = 463 m/s l'énergie mécanique vaut : Esol = -GMm/R + ½mvlib2 L'énergie mécanique à une distance infinie est nulle d'où : ½mvlib2 = GMm/R vlib2 = 2MG/R ; vlib =[2MG/R]½. Calcul de cette vitesse d’évasion pour un corps quelconque se situant à la surface de la Terre : vlib =[2*5,98 1024*6,67 10-11 / 6,38 106]½=11,2 km/s. L’énergie cinétique moyenne d’agitation des molécules de l’atmosphère terrestre est de l’ordre de Ec = 1,5 kT, où k est la constante de Boltzmann et T la température absolue de l’atmosphère. Calcul de cette énergie cinétique d’agitation pour une température absolue de 300 K : k = 1,38 10-23 J K-1. Ec = 1,5 kT= 1,5* 1,38 10-23 *300 = 6,21 10-21 J. Comparaison à l’énergie cinétique d’une molécule de dioxygène qui s’évaderait de la surface terrestre. masse d'une molécule de dioxygène : m = 0,032 / NA = 0,032 / 6,02 1023 = 5,32 10-26 kg Ec = ½mvlib2 = 0,5*5,32 10-26 *(11,2 103)2 = 3,33 10-18 J. conclusion : la molécule de
dioxygène ne peut pas être
libérée de l'attraction terrestre ; cette
molécule reste au voisinage de la Terre.
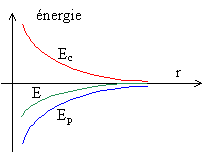
Expression l’énergie mécanique E d’un satellite en orbite terrestre en fonction de G, M, m et r : ( r= R+h) E= Ep+Ec = ½mv2 - GMm/r or v2 = GM/r d'où E= - ½GMm/r Relation entre E et Ec : E= -Ec ; relation entre E et Ep : E =½ Ep . Allure des courbes Ec ,
Ep , E en fonction de r : Un satellite d’observation évolue sur une orbite circulaire très basse (h = 180 km), ce qui permet de discerner des détails d’environ un mètre sur la Terre. Par suite des collisions avec les molécules de l’air des couches supérieures de l’atmosphère, le satellite est soumis à une force de frottement f de norme f=bmv2/ h où h représente l’altitude, m la masse du satellite, v sa vitesse et ß une constante valant 10-8 S.I. L'énergie mécanique du satellite freiné par l’atmosphère diminue du travail de f. Or E= -Ec=-½mv2 ; si E diminue alors la vitesse du satellite augmente. Or E=-½Ep = -½mGM/r ; si E diminue alors la distance r diminue. Expression approchée de la variation Dh du satellite après une révolution : D'une part E= - ½mGM/r d'où D E= ½mGM/r2 Dr. D'autre part D E= travail de la force de frottement de valeur f=bmv2/ h Travail de cette force durant un tour ( 2pr) : -bmv2 2pr / h Par suite : ½mGM/r2 Dr = -bmv2 2pr / h ; ½GM/r2 Dr =- bv2 2pr / h Or v2 = GM/r d'où 1/(2r) Dr =- b 2pr / h ; Dr = -4b pr2/h. AN : Dr = -4 10-8*3,14 * (6,38 106 +1,8 105)2 / 1,8 105 = 30 m. |
|||
|
|
|||
|
|