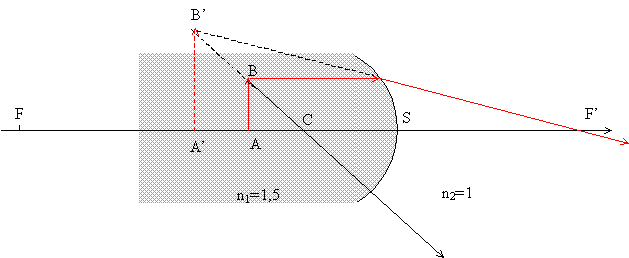
dioptres sphériques : constructions d'images ; relation de conjugaison d'après LSTA 1^ère année.

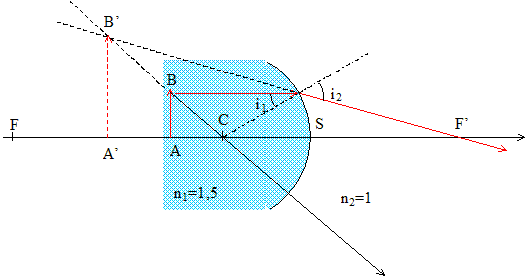
( on écrit en bleu et en gras les distances algébriques)

foyer image F':

Le foyer image d'un système optique est le point conjugué du point du milieu objet situé à l'infini sur l'axe principal.

n₁/CA'-n₂/CA=(n₁-n₂)/CS avec (n₁-n₂)/CS =0,5/0,03=50/3=16,67.

l'objet étant à l'infini, n₂/CA =0 d'où n₁/CF'=50/3 ; CF'=3n₁/50 =3*1,5/50=0,09 = 9 cm

Le foyer objet F est symétrique de F' par rapport au milieu du segment SC joignant le sommet S au centre géométrique C du dioptre.

position de l'image A'B':

n₁/CA'-n₂/CA=(n₁-n₂)/CS= 50/3 avec CA=-0,02 m

n₁/CA'=50/3+n₂/CA=50/3 + 1/(-0,02)=50/3-50=-100/3 ; CA'=-3n₁/100=-4,5/100=-0,045 m=-4,5 cm.

nature de l'image : A'B' étant située à gauche du dioptre est virtuelle.

taille de l'image : A'B' / AB = A'C/AC ; A'B' =AB *A'C/AC =AB*4,5/2 = 2,25 AB.

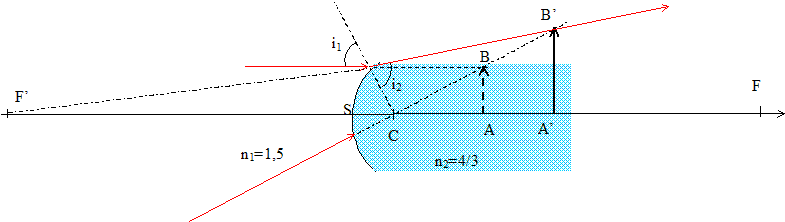
( on écrit en bleu et en gras les distances algébriques)

foyer image F':

Le foyer image d'un système optique est le point conjugué du point du milieu objet situé à l'infini sur l'axe principal.

n₁/CA'-n₂/CA=(n₁-n₂)/CS avec (n₁-n₂)/CS =(1,5-4/3)/(-0,03)=-0,5/0,09=-50/9=-5,56.

l'objet étant à l'infini, n₂/CA =0 d'où n₁/CF'=-50/9 ; CF'=-9n₁/50 -9*1,5/50=-0,27 = -27 cm

Le foyer objet F est symétrique de F' par rapport au milieu du segment SC.

position de l'image A'B':

n₁/CA'-n₂/CA=(n₁-n₂)/CS= -50/9 avec CA=+0,06 m

n₁/CA'=-50/9+n₂/CA=-50/9 + 4/(3*0,06)=150/9=50/3 ; CA'=+3n₁/50=3*1,5/50=+0,09 m=+9 cm.

nature de l'image : A'B' étant située à droite du dioptre est réelle.

taille de l'image : A'B' / AB = CA'/CA ; A'B' =AB *CA'/CA =AB*9/6 = 1,5 AB.

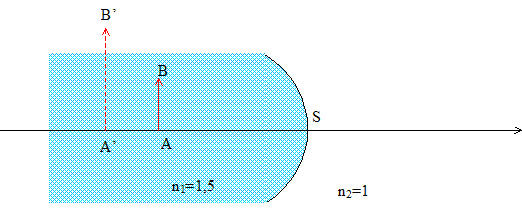
Le dioptre placé en S sépare deux milieux (1) et (2) dont l'un est le verre ( n₁=1,5) et l'autre est l'air (n₂=1). La lumière se déplace de la gauche vers la droite.

On donne objet réel AB=1 cm ; image virtuelle A'B'= 2 cm ; AS= 9 cm ; A'S= 12 cm.

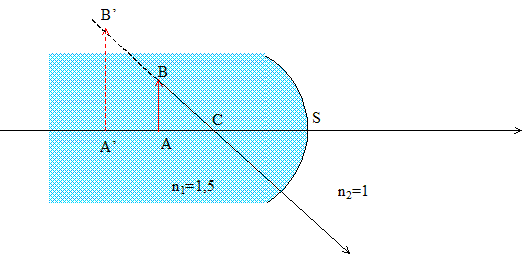
L'intersection de la droite (B'B) avec l'axe A'A donne C :( un rayon issu de B et passant par C n'est pas dévié)

A'B'/AB =A'C/AC d'où AC=A'C*AB/A'B' =0,5 A'C (A milieu de A'C)

de plus A'A= 3 cm d'où AC=3 cm et CS= 9-3 = 6 cm = 0,06 m

vergence de ce dioptre : (n₁-n₂)/CS= 0,5/0,06 =50/6 = 8,33 m^-1.

Foyers :

Le foyer image d'un système optique est le point conjugué du point du milieu objet situé à l'infini sur l'axe principal.

n₁/CA'-n₂/CA=(n₁-n₂)/CS avec (n₁-n₂)/CS =50/6.

l'objet étant à l'infini, n₂/CA =0 d'où n₁/CF'=50/6; CF'=6n₁/50 =0,18=18 cm

Le foyer objet F est symétrique de F' par rapport au milieu du segment SC.