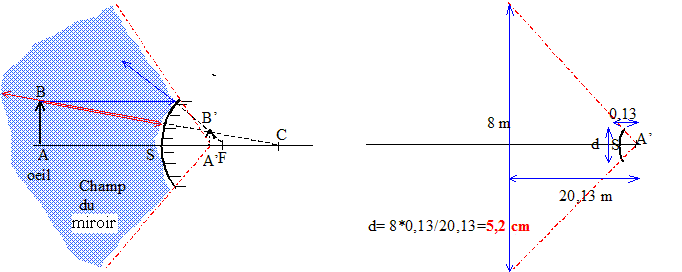miroirs sphériques : constructions d'images ; relation de conjugaison d'après LSTA 1^ère année.

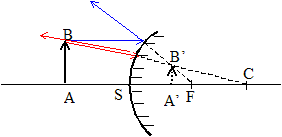
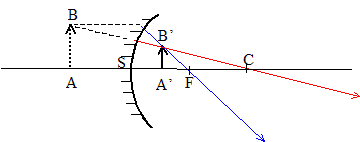
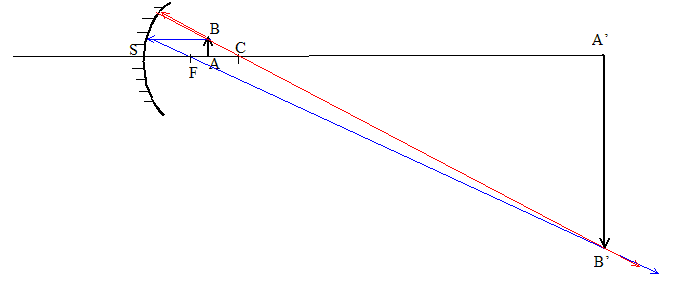
Caractéristiques de l'image A'B' d'un objet AB réel mesurant 1 cm, situé à 2 m du sommet, donnée par un miroir sphérique convexe ( R=4 m)

calculs ( on écrit en bleu et en gras les distances algébriques) position :1/SA'-1/SA=-2/SC avec SC=4 ; SA=-2 1/SA' =-2/SC +1/SA=-2/4+1/(-2)=-0,5-0,5 = -1 SA' = -1 : image virtuelle située 1 m à droite de S grandissement : g=SA' /SA=-1/-2 =+0,5 taille de l'image : 0,5 cm sens : le même que l'objet

construction

calculs ( on écrit en bleu et en gras les distances algébriques) position :1/SA'-1/SA=-2/SC avec SC=4 ; SA=6 1/SA' =-2/SC +1/SA=-2/4+1/6=-3/6+1/6=-2/6=-1/3 SA' = -3 : image virtuelle située 3 m à droite de S grandissement : g=SA' /SA=-3/6 =-0,5 taille de l'image : 0,5 cm sens : inversé par raport à l'objet

construction un rayon (ou son prolongement), issu de B, passant par C, n'est pas dévié après réflexion. un rayon (ou son prolongement), issu de B, parallèle à l'axe optique, émerge après réflexion en passant par F.

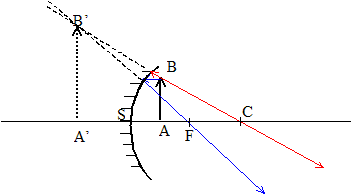
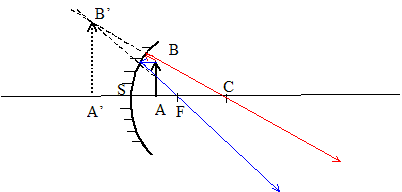
Caractéristiques de l'image A'B' d'un objet AB réel mesurant 1 cm, situé à 1 m du sommet, donnée par un miroir sphérique concave ( R=4 m)

calculs ( on écrit en bleu et en gras les distances algébriques) position :1/SA'-1/SA=-2/SC avec SC=-4 ; SA=-1 1/SA' =-2/SC +1/SA=-2/(-4)+1/(-1)=0,5-1 =-0,5 SA' = -2: image virtuelle située 2 m à gauche de S grandissement : g=SA' /SA=-2/-1 =+2 taille de l'image : 2 cm sens : le même que l'objet

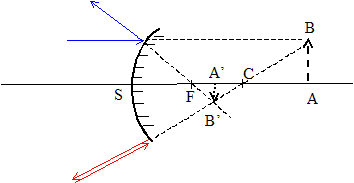
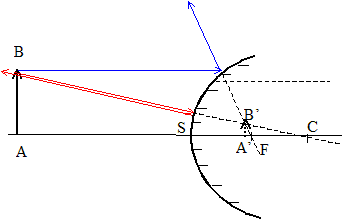
construction un rayon (ou son prolongement), issu de B, passant par C, n'est pas dévié après réflexion. un rayon (ou son prolongement), issu de B, parallèle à l'axe optique, émerge après réflexion en passant par F

Caractéristiques de l'image A'B' d'un objet AB virtuel mesurant 1 cm, situé à 2 m du sommet, donnée par un miroir sphérique concave ( R=4 m)

calculs ( on écrit en bleu et en gras les distances algébriques) position :1/SA'-1/SA=-2/SC avec SC=-4 ; SA=2 1/SA' =-2/SC +1/SA=-2/(-4)+1/2=0,5+0,5=1 SA' = 2: image relle située 1 m à droite de S grandissement : g=SA' /SA=1/2 =+0,5 taille de l'image : 0,5 cm sens : le même que l'objet

construction un rayon (ou son prolongement), issu de B, passant par C, n'est pas dévié après réflexion. un rayon (ou son prolongement), issu de B, parallèle à l'axe optique, émerge après réflexion en passant par F

Un miroir sphérique ( R=0,2 m) projette l'image de la flamme d'une bougie sur un écran placé à 1 m du sommet. Quel miroir choisir ? Où faut-il placer la bougie ? Quelle est la taille de l'image ?

L'image étant obtenue sur un écran est réelle : donc située 1 m à droite du sommet du miroir.

 calculs

( on écrit en bleu et en gras les distances algébriques)

position :1/SA'-1/SA=-2/SC avec SC=-0,2 ; SA'=+1

1/SA =+2/SC +1/SA'=+2/(-0,2)+1/1)=-10+1 =-9

SA = 1/(-9)=-0,11 m: objet réel situé 11 cm à droite de S

grandissement : g=SA' /SA=1/(-0,11) =-9

taille de l'image : 9 fois plus gande que l'objet

sens : inverse par rapport à l'objet

Le miroir du dentiste est monté à l'extrémité d'une tige. L'image doit être droite. Lorsque le miroir st situé à 1,5 cm d'une dent, l'image doit être deux fois plus grande.

Quelles sont les caractéristiques du miroir ?

L'image n'est pas obtenue sur un écran, mais observée par l'oeil : elle est virtuelle, située à gauche du miroir. Elle joue le rôle d'objet pour l'oeil ; l'image définitive se forme sur la rétine. 

Le kératomètre est un dispositif permettant de mesurer le rayon de courbure de la cornée de l'oeil. On peut ainsi choisir sur mesure ces lentilles de contact. La cornée se comporte comme un miroir convexe. Un objet réel est placé à 96 mm de l'oeil. L'instrument permet de mesurer la taille de l'image virtuelle. Si le grandissement est 0,04, quel est le rayon de courbure de la cornée ?

L'objet est réel, situé à gauche du miroir convexe. Le grandissement étant positif, l'image a le même sens que l'objet. L'image est virtuelle, située à droite du miroir.

Un satellite terrestre sphérique a un diamètre D= 2 m et se trouve à une altitude h=500 km. il est observé par un télescope constitué d'un miroir sphérique concave de rayon R = 1 m. Où se trouve l'image du satellite et quelle est sa taille ?

Le satellite est considéré à l'infini (SA>>SC).

1/SA'-1/SA=-2/SC conduit à : 1/SA' =-2/SC. L'image se trouve donc au foyer F.

diamètre apparent a = diamètre du satellite / distance observateur-satellite

a=2/500 000 = 4 10^-6 rad.

de plus a= taille de l'image / distance focale SF

taille de l'image =distance focale SF* a=½Ra = 0,5*4 10^-6 =2 10^-6 m.

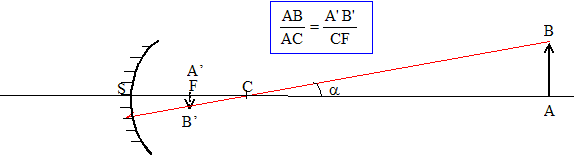
Un rétroviseur est constitué d'un miroir convexe de rayon R= 40 cm. L'oeil de l'observateur se trouve à 40 cm du sommet. Quel est le diamètre de ce miroir pour que l'observateur puisse voir entièrement les trotoirs d'une rue de 8 m de large 20 m derrière lui ? Qu'obtiendrait-on avec un miroir plan placé au même endroit ?

Le champ d'un miroir est la région de l'espace vue par un observateur à travers le miroir. Il est défini par le cône qui s'appuie sur le contour du miroir et dont le sommet est l'image de l'oeil de l'observateur. Ce champ augmente lorsque la distance oeil-miroir diminue.

Recherchons l'image de l'oeil :

L'objet, l'oeil est situé à SA=-0,4 m ; SC=+0,4 m ;

1/SA'-1/SA=-2/SC donne : 1/SA'=-2/SC+1/SA=-2/0,4+1/(-0,4)=-3/0,4 ; SA' =-0,13 m

La largeur de la rue, à 20 m à l'arrière, visible dans le champ du miroir, serait : 0,052*20,4/0,4=2,7 m.