Aurélie 21/12/06
 

Bernoulli ; Archimède ; Poiseuille d'après LSTA 1ère année.

Google

Archimède

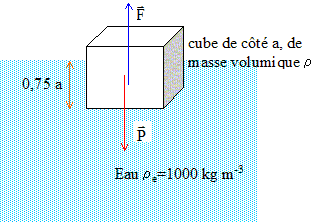
Calcul de la masse volumique du cube :

Le cube est en équilibre sous l'action de deux forces opposées : le poids P=mg et la poussée d'Archimède F, de valeur égale au poids du volume d'eau déplacé.

masse ( kg) = masse volumique ( kg/m3) * volume du cube = ra3.

P= mg =ra3g

volume immergé : (0,75 a)3 ; poussée F=(0,75 a)3re g

par suite : ra3g =(0,75 a)3re g ; r = 0,753re =0,753*1000 =7,53= 422 kg m-3.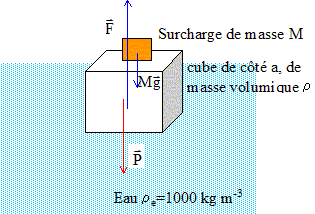

Le cube est entièrement immergé, sans couler.

Calcul de M : ( on donne a = 0,1 m)

Le cube est en équilibre sous l'action de deux forces opposées : les poids P=(M+m)g et la poussée d'Archimède F, de valeur égale au poids du volume d'eau déplacé.

(M+ra3)g = a3re g ; M= a3(re-r) = 10-3(1000-422) =0,578 kg.

Pression due à l'eau sur la face inférieure du cube : ( g= 10 m/s²)

pression à la base d'une colonne d'eau de hauteur a= 0,1 m

p= reg a = 1000*10*0,1 = 1000 Pa.

Force pressante exercée par l'eau sur la face inférieure du cube :

force (N) = pression (Pa) * surface (m2)

force = 1000 * 10-2 = 10 N.
Bernoulli

Une chaudière placée dans une cave envoie de l'eau dans une canalisation d'un chaufage central. L'eau est considérée comme un fluide parfait. L'eau quitte la chaudière par un tuyau de rayon r0=2 cm, à la vitesse v0= 1m/s sous la pression p0=3 bars.

A une hauteur H= 6 m au dessus de la chaudière, l'eau circule dans un tuyau de rayon r = 1 cm.

Donnée : masse volumique de l'eau : r= 1000 kg m-3.
Calcul de la vitesse et de la pression de l'eau à la hauteur H :

conservation du débit volumique : débit ( m3/s) = section (m2) * vitesse m/s)

pr02 v0 = p r2v soit v = (r0/r)2 v0 =4*1 ; v= 4 m/s.

Relation de Bernoulli : p/r + gz + ½v² = constante. g représente la valeur du champ de pesanteur terrestre.

Appliquer cette relation entre A ( chaudière) et B ( altitude H):

état A : pression p0 ; altitude nulle, vitesse v0.

état B : pression p ; altitude H, vitesse v.

p0 /r + 0 + ½v0² =p/r + gH + ½v²

p= p0 + ½r(v0²- v²)-rgH ; p = 3 105+500(1-4²)-10000*6 = 2,32 105 Pa ; p = 2,32 bars.

en absence de circulation d'eau : p0 -p =rgH = 10000*6 = 6 104 Pa ; p = 0,6 bars.
 
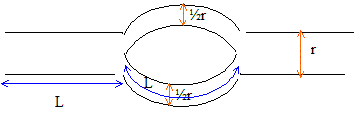
débit si écoulement laminaire : loi de Poiseuille

Une perte de pression Dp apparaît entre deux points distants d'une longueur l d’une canalisation de rayon r, dans laquelle un fluide circule à la vitesse moyenne v , avec un débit volumique qv constant. La viscosité h est constante à pression et température fixées.

D'autre part : débit ( m3/s) = section (m2) * vitesse m/s) ; qv = pr2 v

Le tuyau principal de rayon r, se dépare en deux tuyaux identiques de longueur L et de rayon ½r.

v1 vitesse moyenne dans un tuyau dérivé ; qv1 = p(½r)2 v1 débit dans un tuyau dérivé.

Conservation du débit : qv = pr2 v = 2p(½r)2 v1 d'où v1 = 2 v.

perte de charge (Pa) = résistance hydraulique fois débit ( m3/s)

loi de Poiseuille ( écoulement laminaire) : Dp = 8h L/ (pr4) qv.

résistance hydraulique du tuyau principal : Rh= 8h L/ (pr4) : L et r exprimés en mètres ;

résistance hydraulique d'un tuyau dérivé : Rh 1= 8h L/ (p(½r)4) = 8h L/ (pr4)*16 =16 Rh

2 tuyaux en parallèle : les débits s'ajoutent soit qv = 2Dp /Rh 1=2Dp /(16Rh) =Dp /(8Rh)

Dp =8 qv Rh .

retour -menu