|
enseignement - agrégation interne 2006 : interféromètre de Michelson |
|||
|
|||
|
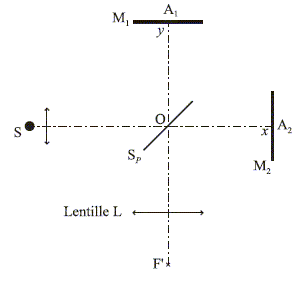
Les interférences à deux ondes sont produites par des dispositifs à division du front d'onde ou des dispositifs à division d'amplitude. Un interféromètre de Michelson est constitué d'une lame semi-réfléchissante, non absorbante, appelée séparatrice Sp dont les facteurs de transmission et de réflexion sur les amplitudes valent ½ et de deux miroirs plans M1 et M2 perpendiculaires l'un à l'autre. L'interféromètre est plongé dans l'air d'indice 1,0000. On utilise comme source étendue une lampe spectrale de symétrie de révolution autour de l'axe SO parallèle à l'axe Ox. On observe en lumière monochromatique dans le plan focal d'une lentille mince convergente L d'axe optique Oy et de distance focale f' = 1,0 m.
Les deux bras OA1 et OA2 étant égaux, on observe une teinte uniforme ou " teinte plate ". La lentille est diaphragmée ( on élimine les rayons incidents trop inclinés sur l'axe ) ; on est alors dans les conditions de Gauss, d'obtention de bonnes images. On déplace M2 normalement à son plan d'une distance e = 1,050 mm dans la direction des x positifs. On observe un phénomène d'interférences analogue à celui d'une lame d'air à faces parallèles.
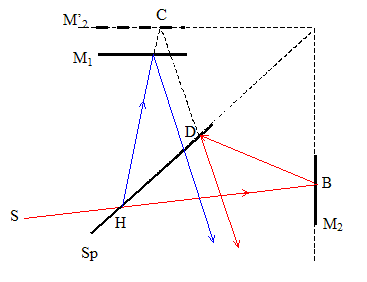
M'2 image de M2 donnée par Sp : M'2 et M2 sont symétriques par rapport à Sp. En conséquence HB= HC et BD= CD. L'interféromètre est donc équivalent à une lame d'air d'épaisseur e= M1M'2. Les rayons réfléchis émergents sont parallèles ; ces derniers interfèrent à l'infini. L'image d'un objet à l'infini se trouve dans le plan focal image de la lentille convergente. La symétrie du dispositif conduit à des franges d'interférences qui ont la forme d'anneaux d'axe de révolution Oy. Calcul du rayon du premier anneau brillant correspondant à l = 434,1 nm.
La réflexion entraîne un déphasage supplémentaire p : d'où F = 2p/l [2e cos i ]+ p. Pour des angles petits, on peut remplacer cos i par un développement limité au 2ème ordre : cos i proche de 1-½i2. F = 2p/l [2e (1-½i2)]+ p Les rayons des anneaux brillants correspondent aux angles d'incidence i tels que l'ordre d'interférences p soit entier. L'ordre d'interférences p =F /(2p) vaut : p =[2e/l (1-½i2)]+½. Pour i = 0 l'ordre d'interférences vaut p0 = 2e/l +½= 2*1,05 10-3 / 434,1 10-9 +0,5= 4838. Au centre l'ordre d'interférence est maximal. L'ordre interférence est p1 pour le premier anneau. p0-p1 = ½ p0i2= 2418,8 i2 ; i = [2(p0-p1) / p0]½. De plus, d'après la figure ci-dessus : tan i = r/f et si l'angle i est petit : r = f i ( f : distance focale de la lentille. r = f [2(p0-p1) / p0]½.
|
|||
|
|
|||
|
|