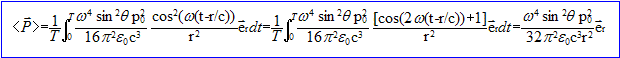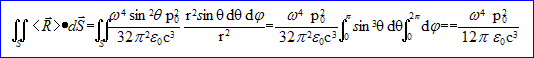Agrégation interne 2006 : champ électromagnétique rayonné pâr un dipôle oscillant.

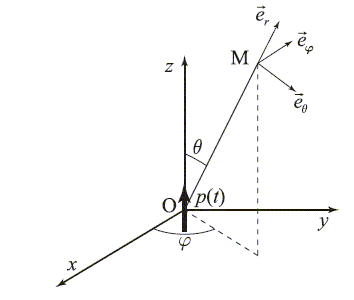
Pour r=OM >> l=2pc/w, le champ magnétique rayonné en M par un dipôle oscillant, de moment dipolaire p(t) = p₀ cos (wt) e_z, placé en un point O est tel que :

E_q= -w² sinq/( 4pe₀rc²) p₀ cos(w(t-r/c)) ; B_j= E_q /c.

Les autres composantes sont négligeables.

Le dipôle ( deux charges +q et - q situées à la distance d ) est équivalent à un élément de courant ldq/dt e_z = dp/dt e_z.

Tout plan contenant l'axe Oz est plan de symétrie.

Le champ électrique est dans le plan défini par Oz et e_q.

Le champ magnétique créé B_j est perpendiculaire au plan contenant le champ électrique.

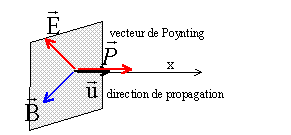
Le rapport des amplitudes E_q / B_j= c est constant et de plus les champs B_j et E_q sont perpendiculaires et transversaux : l'onde est dite " quasi-plane".

P = E^B / m₀ avec E = -w² sinq/( 4pe₀rc²) p₀ cos(w(t-r/c)) e_q =E_qe_q B = E_q /c e_j.

P =E_q e_q ^E_q /(cm₀) e_j = E²_q/(cm₀)e_q ^e_j =E²_q/(cm₀)e_r .

P =[w² sinq/( 4pe₀rc²) p₀ cos(w(t-r/c))]² /(cm₀) e_r avec 1/(cm₀) = e₀c

P = w⁴ sin²q/( 16p²e₀r²c³) p²₀ cos²(w(t-r/c))e_r .

Valeur moyenne de <P> sur une période :

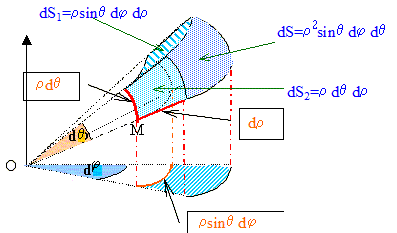
L'énergie moyenne rayonnée par unité de temps à travers la sphère de tayon r, c'est à dire le flux de P à travers la surface de la sphère de rayon r vaut :

Primitive de sin³q :

sin³q = sinq* sin²q = sinq*(1-cos²q ) = sinq-sinqcos²q.

primitive de sin q : -cos q dont la valeur entre 0 et p est : 2.

primitive de -sinq cos²q : u = cosq ; u '= - sinq ; -sinq cos²q = u²u' d'où la primitive : 1/3u³ = 1/3cos³q.

la valeur de 1/3cos³q entre 0 et p est : -2/3