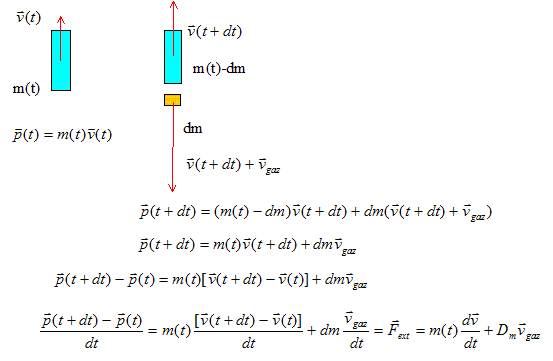|
Agrégation 2006 : moteurs thermiques ; propulsion chimique d'une fusée. |
|||
|
|||
|
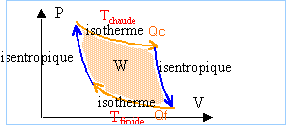
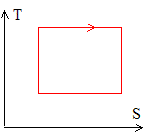
La variation d'entropie est nulle sur le cycle : DS=0 ; par suite Q/Tsource <=0 soit Q<=0 La variation d'énergie interne est nulle sur le cycle : DU=W+Q=0 ; d'où W=-Q Q
étant négatif ou nul, alors le travail W est
positif : ce type de moteur ne peut pas fournir de travail
au milieu extérieur.
Ordre de grandeur du travail mis en jeu sur un cycle W= Phaute V = 3 106 * 10-3 = 3 103 J/ cycle. Considérons une vitesse de rotation de 1500 tours/min soit 25 tours/s ( 25 cycles par seconde) Orde de grandeur de la puissance mise en jeu : 25*3 103 = 75 kW.
Sur le cycle, le 2ème principe s'écrit : DS=0 soit Qf/Tf+Qc/Tc<=0, relation vérifiée si Qc>0 et Qf<0, Tf étant inférieure à Tc. rendement h= |W| /Qc =(Qf+Qc)/Qc = 1 +Qf /Qc avec dans le cas de la réversibilité : Qf/Tf+Qc/Tc=0 ; Qf /Qc = -Tf /Tc ; par suite h= 1-Tf /Tc. Le rendement est d'autant plus proche de 1 que l'écart des températures est grand. Ce moteur manque de puissance car il met en jeu des processus isothermes qui sont lents.
La température de la source froide, l'eau d'un fleuve, est voisine de 10°C soit Tf=283 K. Le rendement maximum est alors :h= 1-Tf /Tc = 1-283/603 =0,53. Le rendement réel est de l'ordre de 0,33 ; près des 2/3 de la puissance de la source chaude est donc perdue. La puissance thermique perdue est de l'ordre de 2 GW. Celle-ci peut être utlisée pour le chauffage urbain, par exemple. |
|||
|
Dans la chambre de combustion, la combustion du propergol amène le gaz à haute température et à haute pression. Il est ensuite détendu dans une tuyère afin d'assurer la propulsion. Une liaison chimique entre deux atomes est modélisée par l'interaction de deux ions dont les charges sont élémentaires et opposées, distantes de d0 = 2 10-10 m Energie potentielle résultant de cette interaction : Ep= 1/4pe0)e2/d0 =9 109 e2/d0 =9 109(1,6 10-19 )2 / 2 10-10 = 10-18 J. Soit par mole : EpNA= 10-18*6 1023 = 6 105 J/mol =600 kJ/mol Du même ordre de grandeur que l'énergie
d'une liaison de covalence.
DT= E/(NAk)=105/(6 1023*1,38 10-23)=1,2 104 K La vitesse d'éjection des gaz vgaz à la sortie de la tuyère est de l'ordre de : Dans la tuyère les gaz se détendent : l'énergie est convertie en énergie cinétique : E = ½mvgaz2 avec m de l'ordre de quelques centièmes de kg. vgaz2 est de l'ordre de 105 / 10-2 = 107 ; vgaz proche de 3 103 m/s
Expression de la force propulsive F : En dt seconde, une masse dm de gaz est éjecté à la vitesse vgaz ; la masse de la fusée devient m-dm ; la vitesse de la fusée est notée v.
La valeur de la force propulsive vaut : Dmvgaz. Au décollage cette force propulsive doit être supérieure au poids initial Mg de la fusée ; d'où le débit massique minimum : Mg/vgaz. On admet que les propergols constituent l'essentiel de la masse de la fusée. Le temps de poussée des propulseurs chimiques est égal à la durée de vidage des réservoirs soit t= M/Dm=vgaz/g = 3 103 /10 = 300 s.
|
|||
|
|