Agrégation 2006 : les principes de la thermodynamique

Enoncé du premier principe ( pour un système fermé ) ou pricipe de conservation de l'énergie :

Un système fermé évolue de l'état 1 à l'état 2 sous l'action des transferts mécanique W_ext et thermique Q :

Le transfert mécanique W_ext ne tient compte que des travaux des forces extérieures.

DE + DU = W_ext+Q avec DE : variation de l'énergie mécanique et DU : variation de l'énergie interne.

Enoncé du théorème de l'énergie cinétique, entre deux instants pour un système fermé :

La variation de l'énergie cinétique entre deux intants de dates t₁ et t₂ est égale à la somme des travaux des forces extérieures et intérieures agissant entre ces deux instants.

DE_c = W_ext+W_int.

par suite DU= Q-W_int : l'énergie interne reste constante s'il ni a ni échange thermique, ni force intérieure.

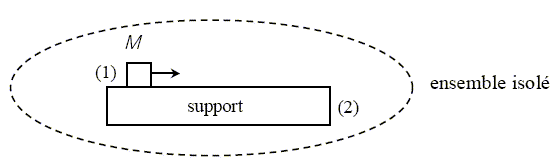
solide (1) : le théorème de l'énergie cinétique s'écrit : 0-½Mv₀² = - mMgL

le premier principe s'écrit : DE₁+DU₁= - mMgL +Q₁ d'où : DU₁=Q₁

support (2) immobile : le théorème de l'énergie cinétique s'écrit : 0 = 0

le premier principe s'écrit : DE₂+DU₂= 0 +Q₂ d'où : DU₂=Q₂

ensemble isolé : le théorème de l'énergie cinétique s'écrit : 0-½Mv₀² = - mMgL

le premier principe s'écrit : DE₁+DU₁+DU₂= 0 ; -½Mv₀² +DU₁+DU₂= 0 ; -½Mv₀² +Q₁ +Q₂ =0 ; ½Mv₀² = Q₁ +Q₂

Le travail des frottements convertit l'énergie cinétique en énergie thermique : la température du solide et du support s'élève.

La puissance mise en jeu est P=F v = 10*2 = 20 watts = 20 joules par seconde.

Volume de la couche à chauffer : 200*0,1 = 20 cm³ ; le corps humain étant essentiellement constitué d'eau, la masse de cette couche est de l'ordre de 20 g = 0,02 kg

Energie transférée à cette couche à chaque seconde : 20 J = 0,02 cDq ; Dq = 20/(0,02*4180)=0,24 degré

En se frottant les mains pendant 1 min, la température s'élève d'environ 14 degrés.

Enoncé pour un système isolé :

L'entropie d'un système isolé ne peut qu'augmenter jusqu'à une valeur maximale, correspondant à un état d'équilibre.

Expression de l'entropie d'un gaz parfait de coefficient g constant en fonction du volume V et de la température T:

dS= dU/T+P/T dV avec P/T = nR/V et dU=nC_vdT = nR/(g-1) dT

d'où dS= nR/(g-1) d (lnT) + nR d(ln V)

par intégration : S-S₀= nR[1/(g-1) ln(T/T₀) + ln(V/V₀)]

Expression statistique de l'entropie : ( Boltzmann) S= k ln W.

W : nombre de micro-états correspondants à un état macroscopique donné.

Le système isolé doit posséder une énergie constante.

Une détente de Joule Gay-Lussac dans le vide double le volume du gaz parfait :

détente adiabatique irréversible : le transfert thermique Q est donc nul.

Système indéformable : le travail des forces de pression W est nul

en conséquence DU = 0 ; l'énergie interne est constante.

Or l'énergie interne d'un gaz parfait ne dépend que de la température : si DU = 0, la température du gaz reste constante

S-S₀= nR ln(V/V₀)= nR ln 2.

Si de l'huile est mise dans l'eau, elle remonte à la surface pour former deux phases bien distinctes ( l'ordre des particules s'accroît). Le processus étant exothermique, de l'énergie est cédée dans le milieu extérieur ( accroissement du désordre énergétique : ce dernier l'emporte ) L'volution du système est en accord avec le second principe.

A 0 K, l'entropie d'un corps pur est nulle. Les particules sont immobiles ; il existe un seul micro-état ; W=1 et S= k ln W donc S=0.