|
Mesure du coefficient de traînée de différents obstacles concours général 2007 |
||||||||||||||
|
||||||||||||||
|
La forme de l'écoulement d'un fluide autour de la bille dépend de la vitesse v et de la taille d de l'obstacle ( ici le diamètre de la bille), mais aussi de la masse volumique r et de la viscosité h du fluide considéré. Pour caractériser le régime d'écoulement on utilise le nombre sans dimension Re, appelé nombre de Reynolds défini par : Re = r v d /h. Parmi les différents régimes d'écoulement que l'on peut observer, on distingue en particulier : L'écoulement laminaire : Re <1 L'écoulement autour de l'obstacle est symétrique et régulier. La force de frottement fluide est donnée par la formule de Stokes : f = -6p r h v
L'écoulement turbulent : 103<Re<105. L'écoulement est caractérisé par des variations spatio-temporelles importantes et aléatoire de la vitesse du fluide. La force de frottement s'exerçant sur la bille s'écrit : f = -½r CxS v2 u ( u : vecteur unitaire colinéaire à la vitesse et de même sens) Cx est le coefficient de traînée de l'obstacle dans le fluide : Cx = 0,43 pour un obstacle sphérique. S : surface frontale vue par le fluide: pour la bille étudiée : S= pr2.
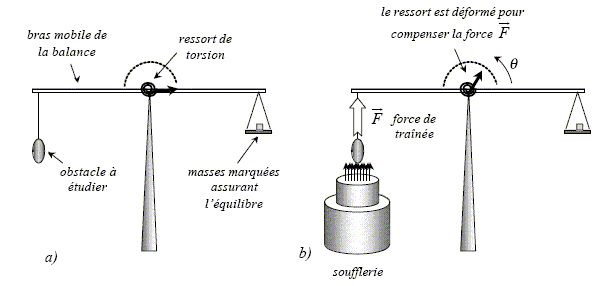
Le coefficient de traînée Cx dépend uniquement du profil aérodynamique de l'obstacle plongé dans l'écoulement et caractérise ainsi l'imlportance de la force de frottement qui s'exerce sur celui-ci. Le dispositif expérimental présenté ci-dessous permet une mesure directe de ce coefficient de traînée : un objet de forme donnée est placé dans un écoulement d'air uniforme ( de vitesse v= 7,0 m/s) crée par une souflerie de laboratoire. La force de traînée F est alors directement compensée par l'action d'un ressort de torsion, déformé par l'expérimentateur d'un angle q par rapport à la situation sans écoulement.
F=
b
q avec b
= 1,0
10-3 N
; q
exprimé en degrés.
On souhaite déterminer le
coefficient de traînée pour chaque profil.
La première étape consiste à caréctériser l'écoulement pour connaître l'exprssion de la force de traînée. L'air est assimilé à un gaz parfait à la température ambiante T0 = 300 K sous la pression atmosphérique P0 = 1,0 105 Pa. On donne la masse molaire de l'air M= 29 10-3 kg /mol et la constante des gaz parfaits R= 8,31 J K-1 mol-1. On considère une masse m d'air contenue dans le volume V. Montrer que la masse volumique de l'air r s'écrit r = MP0/(RT0). Quantité de matière (mol) d'air = masse (kg /) / masse molaire (kg/mol) n = m / M . Définition de la masse volumique ( kg m-3) = masse (kg) / volume ( m3) r = m/V. Equation des gaz parfaits : P0 V = nRT0. P0 V = mRT0/M ; m/V = MP0/(RT0).
r = MP0/(RT0) = 29 10-3 * 105 / (8,31*300) r =1,2 kg m-3. Calculer le diamètre d des obstacles. S= pd2/4 ; d =2 [S/p]½. d = 2 [1,2 10-3/3,14]½ =3,9 10-2 m. Calculer le nombre de Reynolds correspondant. On donne la viscosité de l'air h= 1,8 10-5 Pa s. Re = r v d /h. Re = 1,2*7*3,9 10-2 /1,8 10-5. Re =1,8 104. En déduire l'expression de la force de traînée qui s'exerce sur les obstacles de la part de l'air en écoulement. La valeur du nombre de Reynolds indique que l'écoulement de l'air autour de l'obstacle est "turbulent". D'où l'expression de la
valeur de la force de traînée
:
F=½r
CxS
v2
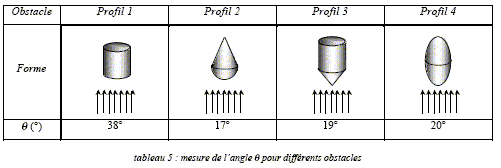
Exprimer le coefficient Cx en fonction de b, q, r, S et v. F=½r CxS v2 = b q. Cx = 2 b q / (rS v2 ). Calculer numériquement Cx pour les obstacles proposés. Cx = 2 b q / (rS v2 ) = 2 10-3 q / (1,2*1,2 10-3 *49) Cx = 2,83 10-2 q.
Classer les obstacles par coefficient de traînée croissante. Conclure.
Le profil en forme de goutte d'eau est le plus aérodynamique.
|
||||||||||||||
|
|
||||||||||||||
|
|