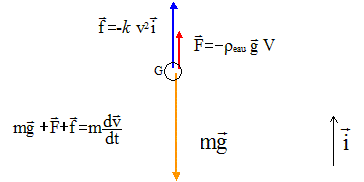Chute d'une bille dans l'eau : méthode d'Euler

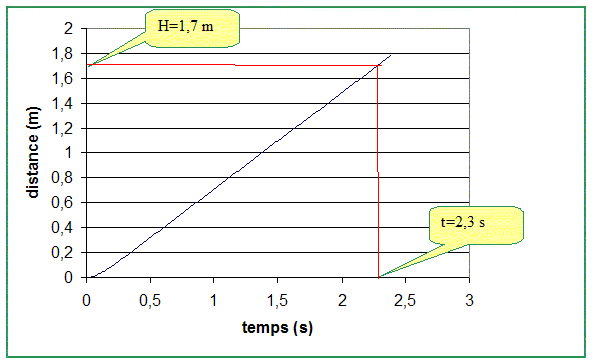
A l'instant du lâcher, la bille est juste immergée dans l'eau. La profondeur de la piscine est h=1,7m.

Elle trouve que la durée de chute est comprise entre 2 et 3 s.

Calculer le temps mis par une bille pour effectuer une chute libre de hauteur h=1,7m.

h= ½gt²

t = [2h/g]^½ = = (3,4/9,8)^½ =0,59 s.

Quelle conclusion doit on tirer pour le mouvement de la bille dans l'eau ?

Dans l'eau le mouvement de la bille n'est pas une chute libre.

La bille est soumise à d'autres forces que son poids.

( en supposant la force de frottement fluide de la forme f=kv² avec k=0,045 unité S.I)

Le bille est soumis à 3 forces:

- la poussée d'Archimède, verticale, orientée vers le haut, valeur = poids du volume de fluide (air) déplacé : F= r_eau V g

avec r_eau : masse volumique de l'eau kg m^-3 ; V : volume de la bille (m³)

- le poids du système, verticale, orientée vers le bas, valeur : P= m g = r_bille V g

- la force de frottement de l''eau sur la bille, verticale, orientée vers le haut, valeur : f = k.v² ( négligeable au début du mouvement car la vitesse est alors très faible)  

Ecrire la seconde loi de Newton :

Ecrire l'équation différentielle du mouvement. Ecrire la seconde loi de Newton suivant un axe verticale ascendant. rbille V g -reau V g - k.v2 = mdv/dt= rbille V dv/dt. dv/dt + k/(rbilleV) v2 =g(1-reau/rbille ).

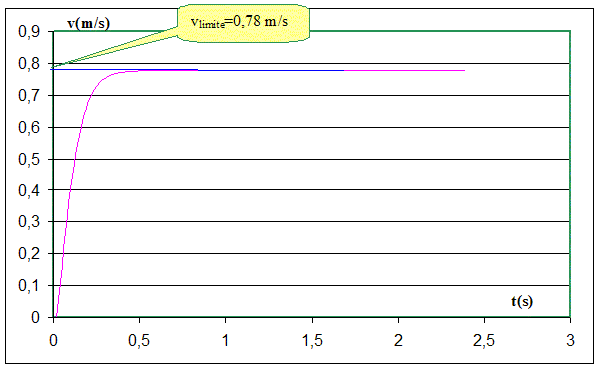
A partir de l'équation différentielle, exprimer, avec des coefficients numériques la variation Dv de la vitesse pour un pas D t=0,01s.

à t=0, la vitesse initiale v₀ est nulle.

r_bille = 2300 kg m^-3 ; r_eau = 1000 kg m^-3 ; k = 0,045 SI ;

V= 4/3 pr³ = 4/3*3,14 ( 8 10^-3)³ = 2,145 10^-6 m³.

k/(r_billeV) = 0,045 /(2300*2,145 10^-6) =9,1.

g(1-r_eau/r_bille ) =9,81(1-1/2,3)=5,5.

Dv = v(t+Dt )- v(t) ;

Dv /Dt +9,1 v² = 5,5 ; Dv /Dt = 5,5-9,1 v²

v(t+Dt )- v(t) = (5,5-9,1 v² )Dt.

Calculer v₁ à t₁=0,01 s puis v₂ à t₂=0,02 s.

v(0,01 )- v(0) = (5,5-9,1 v₀² )Dt.

v₁ = v₀+(5,5-9,1 v₀² )Dt.

v₁ =0+5,5*0,01 = 5,5 10^-2 m/s.

v(0,02 )- v(0,01) = (5,5-9,1 v₁² )Dt.

v₂ = v₁+(5,5-9,1 v₁² )Dt.

v₂ =5,5 10^-2+(5,5-(9,1*(5,5 10^-2)²)*0,01 = 0,11 m/s.

Représenter sur excel, v=f(t) sur l intervealle de temps (0 s ;3s).

v(t+Dt )=v(t) + (5,5-9,1 v(t)² )Dt.

Déduire la vitesse limite v_limite.

v= Dz / Dt.

En déduire Dz.

Dz = v Dt.

z(t+Dt) - z(t) = v Dt.

z(t+Dt) = z(t) + v Dt.

On utilise la méthode des variation d'Euler avec un pas Dt=0,01 s.A t=0,z=z₀=0.

Calculer, à la calculatrice, z₁ à t₁=0,.01s puis z₂ à t₂=,02 s.

z(0,01) = z(0) + v (1)Dt

z₁ = 0 + 0,087 *0,01 = 8,7 10^-4 m.

z₂ = 8,7 10^-4 + 0,11 *0,01 = 2,0 10^-3 m.

Représenter sur excel z=f(t) toujours par pas de 0,01 s sur l intervalle (0s ; 3s ).

Déterminer la durée de la chute.