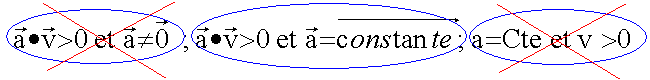|
concours d'entrée médecine dentaire QCM, mouvements uniformes, dipôle RLC entretenu Rabat 2006 |
|||
|
|||
|
- La durée d'une oscillation est l'intervalle de temps qui sépare deux passages successifs du mobile par la même position. Faux. Il faut ajouter " et dans le même sens" pour que cela soit vrai - La loupe donne d'un objet réel, une image réelle droite. Faux. L'image est droite mais virtuelle. - Le microscope contient un système optique formé de deux lentilles une convergente et l'autre divergente. Faux. Les deux lentilles sont convergentes. - La valeur du champ magnétique est proportionnelle à l'intensité du courant qui le produit. Vrai. - L'énergie de l'atome d'hydrogène est quantifiée.Vrai.
Le mouvement d'un mobile est uniformément accéléé si :
La masse m(X) d'un noyau AZX est : - inférieure à Z m(p) + (A-Z)m(n) Vrai. - supérieure à Z m(p) + (A-Z)m(n) - égale à Z m(p) + (A-Z)m(n) Soit T la demi-vie d'un noyau radioactif. Le temps nécessaire pour la désintégration de 75 % d'un échantillon est : t= T ; t= 2T ; t= 3T. A chaque demi-vie ou période la moitié des noyaux initiaux se sont désintégrés. à t= T: 50 % désintégrés, il en reste 50 % A t = 2T : 50% + 50*0,5 %= 75 %
désintégrés.
T0 = 2p (m/k)½ avec m = 0,25 kg. m/k = 0,25/25 = 0,01 ; (m/k)½ = 0,1
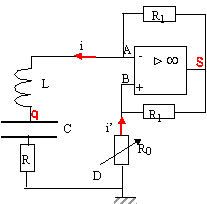
Dans un référentiel terrestre, un mobile autoporteur (S) de masse m= 400 g, a un mouvement circulaire uniforme. Il se déplce sans frottement sur un plan horizontal. Il est relié à un point fixe de la table par un fil inextensible et de masse négligeable. La vitesse du centre d'inertie du mobile est v= 20 cm s-1 et la distance entre le centre et le point fixe est r = 20 cm. Calculer la valeur de la force exercée par le fil sur le mobile. L'accélération est centripète de valeur aN= v2/r. La tension du fil est centripète de valeur T= maN= mv2/r avec m = 0,4 kg, v = 0,2 m s-1 et r = 0,2 m F= 0,4*0,22/0,2 = 0,4*0,2 = 0,08 N. Au cours du mouvement et à un instant t=0 le fil casse. Ecrire l'équation horaire du mouvement ultérieur de l'autoporteur ( à t=0, x=0). Justifier. Sur une table à coussin d'air, après rupture du fil, l'autoporteur est pseudo-isolé. Le mouvement est rectiligne uniforme ( d'après la première loi de Newton) suivant la tangente au cercle à l'instant t=0. x= vt = 0,2 t. On considère un circuit oscillant de type RLC dont les oscillations sont entretenues par un dipôle à résistance négative (-R0).
Montrer que l'équation différentielle de l'évolution de l'oscillateur entretenu peut être écrite : d2uc/dt2 + k uc=0. La partie droite du circuit simule une résistance négaative -R0. Additivité des tensions : uc + Ri + Ldi/dt -R0i =0 avec i= dq/dt et q= Cuc soit i = Cduc/dt et di/dt = C d2uc/dt2. d'où uc +( R-R0)Cduc/dt + LCd2uc/dt2 =0 si R=R0 les oscillations sont entretenues. uc + LCd2uc/dt2 =0 ; d2uc/dt2 + 1/(LC) uc = 0. Nommer la grandeur k et donner son unité S.I. On pose k = (LC)-1. k est une pulsation au carré ; son unité est ( rad s-1)2.
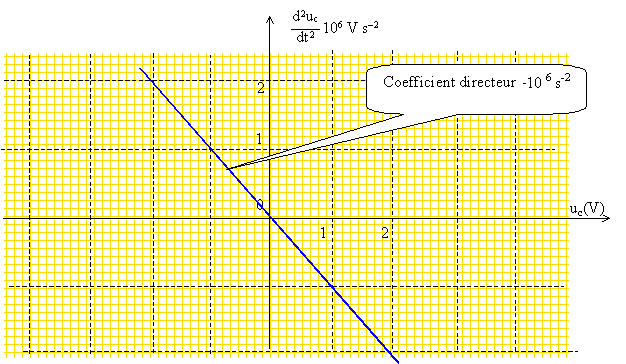
Un logiciel a permis d'obtenir le graphe ci-dessous. Ce graphe est-il en accord avec l'équation différentielle précédente ? Le graphe est en accord avec l'équation différentielle précédente d2uc/dt2 = -kuc. En conséquence k = 106 s-2. En déduire la valeur de la période propre T0 de l'oscillateur. T0 = 2p k-½ = 2p 10-3 s. Exprimer l'énergie totale E de l'oscillateur entretenu et en déduire que [T0/(2p) duc/dt]2 + uc2 = A où A sera exprimé en fonction de E et de la capacité C du condensateur. L'énergie totale E est égale à la somme de l'énergie stockée par le condensateur et de l'énergie stockée par la bobine. E= ½Cuc2 + ½Li2 avec i = Cduc/dt E= ½Cuc2 + ½L (Cduc/dt)2. Or [T0/(2p)]2= k-1 = LC d'où : E= ½Cuc2 + ½ C[T0/(2p)]2( duc/dt)2. [T0/(2p) duc/dt]2 + uc2 = 2E/C =A. |
|||
|
|
|||
|
|