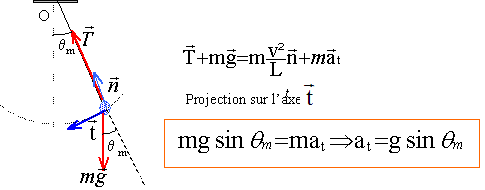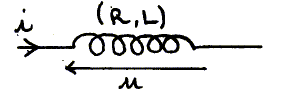Aurélie 23/05/07 23/05/07
 

concours d'entrée médecine physique : projectile ; pendule ;champs électrique et magnétique ; prisme; bobine inductive . Casablanca 2006

durée 30 min.

Google

 

Un projectile ponctuel est lancé à l'instant t=0 d'un point O centre du repère (OXY) avec une vitesse initiale v0 faisant un angle a avec l'axe Oy. On néglige les frottements de l'air et on considère que l'intensité du champ de pesanteur g est constante.

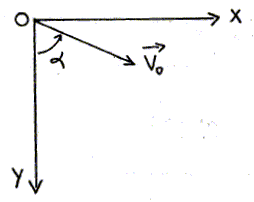
Ecrire l'équation horaire x=f(t) :

Composantes du vecteur accélération : (0 ; g)

Composantes du vecteur vitesse initiale : ( v0 cos a ; v0 sin a ).

Le vecteur vitesse est une primitive du vecteur accélération, d'où les composantes du vecteur vitesse :

( v0 cos a ; gt +v0 sin a )

Le vecteur position est une primitive du vecteur vitesse, d'où les composantes du vecteur position :

x(t) = v0 cos a t.

Ecrire l'équation horaire y=g(t) :

y(t) = ½gt2 + v0 sin a t.

Un pendule simple de longueur L et de masse m oscille sans frottements entre les positions extrèmes A et B. Le pendule est abandonné à l'instant t=0 sans vitesse initiale à partir de la position A et arrive à la position B à l'instant t=1 s.

On donne p2=10, g = 10 m/s² et on considère que l'amplitude qm est faible.

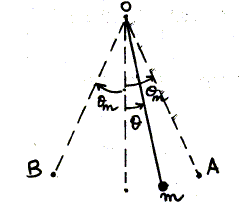
Calculer L :

période du pendule : T= 2p (L/g)½ ;

T2 = 4 p2 L/g ; L = T2 g/( 4 p2 ) avec T= 2 s

L= 4*10/(4*10) = 1 m.

Calculer l'accélération normale aN au point A :

En A la vitesse est nulle ; de plus aN= v2/ L.

En A l'accélération normale est nulle.

Exprimer l'accélération tangentielle aT en fonction de g, qm au point A .

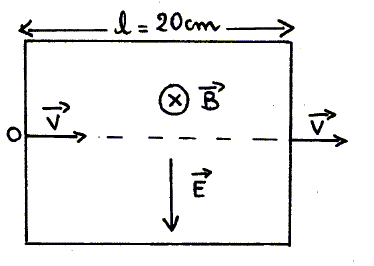
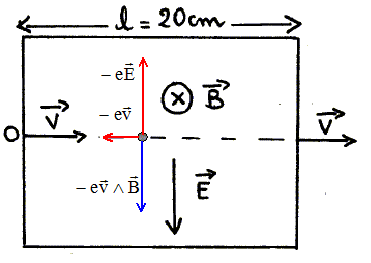
Les vecteurs sont écrits en gras et en bleu.

Un faisceau d'électrons pénètre en O dans une région de longueur l=20 cm où règne un champ électrostatique uniforme de module E = 2 104 V/m et un champ magnétique uniforme B perpendiculaire à E.

Certains électrons traversent cette région selon un mouvement rectiligne uniforme pendant la durée Dt= 2 ms à la vitesse v.

Calculer la vitesse v :

v = l/Dt = 0,2/2 10-6 = 105 m/s.

Exprimer B en fonction de E et v.

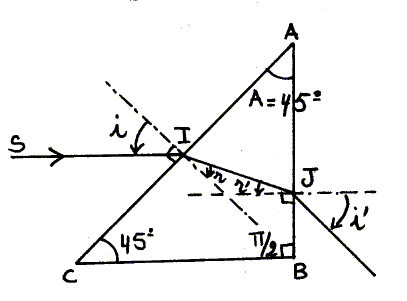
Les électrons sont soumis à deux forces opposées ( principe d'inertie), le poids étant négligeable : la force électrique -eE et la force magnétique -ev^B.

Ces forces ont même valeur : eE=evB soit B= E/v.

B= 2 104 / 105 = 0,2 T.

Un faisceau lumineux monochromatique horizontal SI arrive au point I, parallèlement à la base BC d'un prisme ABC d'angle A= 45° et d'indice de réfraction n = 2½.

sin 30 = 0,5 ; sin 45 = 2-½ ; sin 60 = ½ 3½.

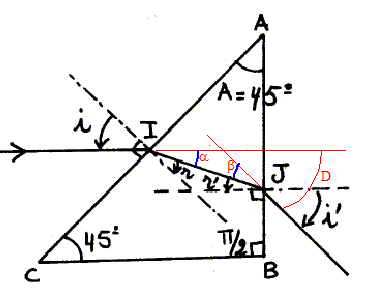
Déterminer l'angle d'incidence i et l'angle de réfraction r au point I.

i = 45° ; nair sin i = n sin r ;

sin r = sin 45/2½ =0,5 ; r = 30°.

Calculer l'angle d'incidence r' au point J.

r+r'=A soit r' = 45-30 = 15°.

Exprimer l'angle de déviation D en fonction de i'.

D= a+b = i-r+i'-r' = 15+i'-15; D= i'.

 

On considère une bobine de résistance R= 20 W et d'inductance L= 0,4 H. On fait passer dans cette bobine un courant électrique d'intensité i variable avec le temps selon :

i(t) = a t avec a = 0,05 A s-1.

Donner la ddp u en fonction de a, R, L et t.

u = Ldi/dt + Ri avec di/dt = a

u = La + R at.

Calculer l'énergie électromagnétique Em à l'instant t= 1 s.

i(t=1) = a = 0,05 A : Em =½L i2 =0,5*0,4*(5 10-2)2 = 5 10-4 J.

retour -menu