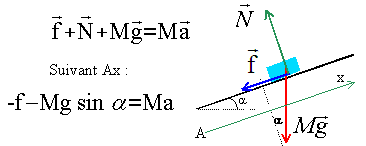concours d'entrée médecine prisme: réfraction ; dipole RLC ; plan incliné ; fission nucléaire ; niveau d'énergie. Casablanca 2006

durée 30 min.

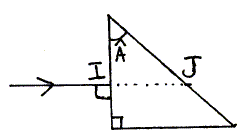
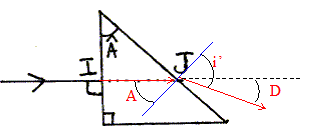
A la sortie de la deuxième face on obtient plusieurs rayons réfractés parmi eux le rayon rouge et le rayon bleu.

Donner l'expression de l'angle de la déviation D en fonction de i' et A. i' : angle de réfraction en J.

D= i'-A.

On donne l'indice de réfraction du prisme pour le rayon rouge n_R= 1,50 et pour le rayon bleu n_B= 1,52.

Calculer sin i'_R, i'_R angle de réfraction pour le rouge en J.

n_Rsin A = sin i'_R ; sin i'_R =1,5*sin 30 = 1,5*0,5 ; sin i'_R = 0,75.

Calculer sin i'_B, i'_B angle de réfraction pour le bleu en J.

n_Bsin A = sin i'_B ; sin i'_B =1,52*sin 30 = 1,52*0,5 ; sin i'_B = 0,76.

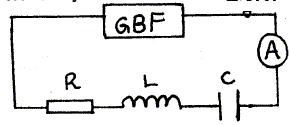
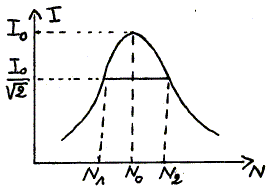
On fait varire la fréquence N et on mesure l'intensité efficace I ; on obtient la courbe suivante:

U= 4,6 V ; I₀ = 20 mA ; N₀ = 580 Hz ; N₁ = 550 Hz ; N₂ = 600 Hz.

Calculer R :

A la résonance d'intensité , l'impédance Z est minimale, égale à R.

R= U/I₀ = 4,6 / 0,02 = 230 W.

Calculer le facteur de qualité Q du circuit :

Q= N₀ / (N₂-N₁)=580/50 = 11,6.

Donner l'expression de l'impédance Z en fonction de R lorsque N=N₂.

Z= U/I avec I= 2^-½ I₀ si N=N₂.

Z = 2^½U/I₀ avec R= U/I₀ ; Z= 2^½R.

Calculer la phase j lorsque N=N₂.

cos j = R/Z ; si N=N₂, Z= 2^½R

d'où cos j =2^-½ = 0,707 ; j = 45° = 0,25 p radian.

Exprimer l'intensité i(t) en fonction du temps lorsque N=N₂.

I = 2^-½ I₀ si N=N₂.

i(t) = I₀ cos ( 2pN₂t + 0,25 p)

Un solide S est lkancé à la vitesse initiale v₀=4 m/s à partir de A le long d'un plan incliné AB faisant un angle a=30° avec l'horizontale. S décrit un mouvement de translation rectiligne. La variation de la vitesse de S est représentée sur la figure 2.

Déterminer graphiquement l'accélération a de ce mouvement.

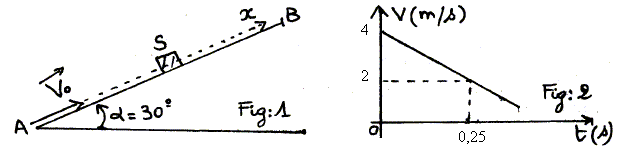
L'accélération est la dérivée de la vitesse par rapport au temps. La vitesse est une fonction affine décroissante.

L'accélération est égale au coefficient directeur de la droite ( fig 2) soit : a = -2/0,25 = - 8 m/s².

A quel instant le solide S s'arrêtera t-il ?

v(t) = -8 t + 4 ; à l'arrêt v=0 soit t =0,5 s.

f est l'intensité de la force de frottement supposée constante et opposée au sens du mouvement.

Donner l'expression de a en fonction de a, g, m et f.

a = -(f/M +g sin a).

Calculer f si a= 30°, m=100 g, g= 10 m/s².

f = m( -a-gsin a) = 0,1(8-10 sin 30 )=0,3 N.

²³⁵₉₂U + ¹₀n--->⁹⁰₃₆Kr +¹⁴²_xBa +y¹₀n

Calculer x et y :

conservation de la charge : 92 = 36 + x soit x =56.

conservation du nombre de nucléons : 235+1 = 90+142+y d'où y = 4.

Calculer la variation de masse Dm en u :

Dm = 3 m(n) + m(Ba) + m(Kr) -m(U) = 3*1,0086 + 141,9163 + 89,9197-235,0439= -0,1821 u.

Calculer en eV l'énergie libérée par cette réaction :

0,1821*931,5 = 169,5 MeV = 1,69 10⁸ eV.

m(Kr)=89,9197 u ; m(Ba) = 141,9163 u ; m(U)=235,0439 u ; m(n) = 1,0086 u ; 1 u = 931,5 MeV/c².

Les niveaux d'énergie de l'atome d'hydrogène sont donnés par E_n=-13,6 /n² ( eV). n entier.

On envoie sur cet atome pris à l'état fondamental successivement trois rayonnement d'énergie respective : E₁ = 8,2 eV, E₂ = 10,2 eV, E₃ = 14,3 eV.

Lequel permet l'ionisation de l'atome ?

L'énergie du photon doit être supérieure à 13,6 eV : donc photon n°3.

Calculer en eV l'énergie cinétique E_c de l'électron éjecté :

E_c = énergie du photon - |énergie de l'atome dans son état fondamental|

E_c = 14,3-13,6 =0,7 eV = 0,7*1,6 10^-19 = 1,12 10^-19 J

Calculer la vitesse de l'électron éjecté : m=9,1 10^-31 kg ; 1 eV= 1,6 10^-19 J.

E_c = ½mv² ; v = (2E_c/m)^½ = (2,24 10^-19 / 9,1 10^-31 )^½ =4,9 10⁵ m/s.