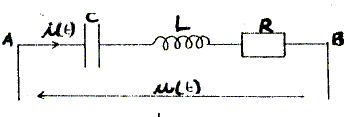Aurélie 24/05/07
 

concours d'entrée médecine lentille, radioactivité, dipole RLC, système de poulies. Casablanca 2004

durée 30 min.

Google

 

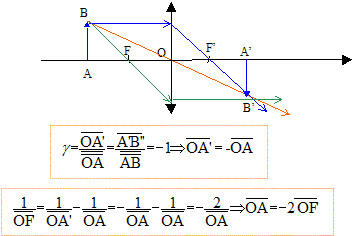
Les distances algébriques sont écrites en gras et en bleu.

Une lentille mince convergente (L) de distance focale OF'= 5 cm donne une image réelle inversée A'B' d'un objet réel AB.

Donner la position OA de l'objet en fonction de OF' si le grandissement est g=-1.

Le noyau d'azote 137N se désintègre en donnant une particule b+ et un noyau AZX.

Identifier A et Z.

137N ---> 01e+ AZX

conservation de la charge : 7=Z+1 d'où Z= 6. (élément carbone)

conservation du nombre de nucléons : A=13.

On dispose d'un échantillon de 137N de masse m0 à l'instant t=0; à l'instant t la masse de l'échantillon est m = 1/8 m0.

Calculer t sachant que la période de désintégration de 137N est T= 10 min.

La masse est divisée par 23 :

Au bout d'une période la masse est divisée par 2 ; au bout de 2 périodes la masse est divisée par 22 ; au bout de 3 périodes la masse est divisée par 23.

t= 3 T = 30 min.

Le schéma suivant représente un dipole RLC série. On applique aux bornes du dipole une tension sinusoïdale u(t) = 6 *2½ cos(1000 t+p/3).

Il est parcouru par un courant électrique i(t) = 0,2*2½ cos(1000 t ). On donne C= 5 mF.

Calculer R :

cos p/3 = R/Z avec Z= U/I = 6/0,2 = 30 W.

R= Zcos p/3 = 30*0,5 = 15 W.

Donner l'expression de L en fonction de Z, R, C et w.

Z2= R2+(Lw-1/Cw)2 ; Z2- R2=(Lw-1/Cw)2.

Lw-1/Cw = (Z2- R2)½.

Lw=1/Cw+ (Z2- R2)½.

L=[ 1/Cw+ (Z2- R2)½] / w.

w= 1000 rad/s ; Z= 30 W ; R= 15 W ; C= 5 10-6 F. L= 0,226 H.

 
On considère deux poulies P1 et P2 accolées, homogènes de masse négligeables et de rayons respectifs R1 et R2. Elles tournent sans frottement autour d'un même axe D.

On entoure autour de P1 un fil inextensible de masse négligeable et on suspend à l'une de ces extrémités un corps (S) de masse m.

Sur l'autre poulie P2 on enroule un autre fil inextensible, de masse négligeable, et on attache son extrémité à un ressort à spires non jointives de raideur k et de longueur à vide L0.
A l'équilibre écrire l'allongement DLé du ressort en fonction de m, R1, R2, k et g.

Système étudié, les poulies : T R2 = T1R1 à l'équilibre.

Système étudié, (S) : T1=mg à l'équilibre.

d'où T R2 = mgR1 ; T= mgR1/R2 ;

or T= k DLé d'où : k DLé= mgR1/R2 ;

DLé= mg/k * R1/R2.

g= 10 N/kg, m=0,1 kg, R1 = 5 cm, R2 = 10 cm, k= 20 N/m.

DLé=0,1*10/20 *5/10 = 0,025 m.
On déplace le corps S de sa position d'équilibre vers le bas d'une distance Xm et on le lâche sans vitesse initiale à l'instant t=0. On considère la position à l'équilibre comme origine des déplacements.

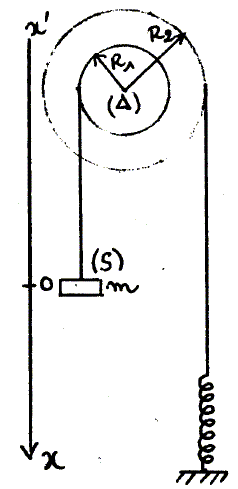
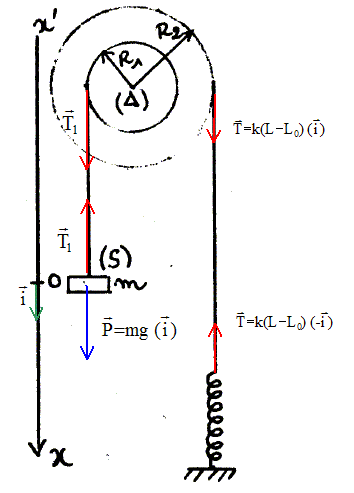
Ecrire l'équation différentielle du mouvement du corps S en fonction de x", x, k, m, R1 et R2.

(S) est soumis à son poids et à la tension du fil T1 = T R2/R1 = k(L-L0) R2/R1

Ecrire la seconde loi de Newton suivant l'axe Ox :

mg - k(L-L0) R2/R1 = mx" (1)

L-L0 = L-Léq +Léq-L0 = L-Léq +DLé ;

k(L-L0) R2/R1 = k(L-Léq) R2/R1 +kDLéR2/R1 avec x = L-Léq.

(1) s'écrit : mg-kR2/R1 x- kDLéR2/R1 =mx"

or DLé= mg/k * R1/R2 d'où : mx" + kR2/R1 x =0

x" + k/m R2/R1 x =0.

Donner l'expression de la pulsation w0 en fonction de k, m, R1 et R2.

w0 =[k/m *R2/R1]½.

Calculer w0.

w0 =[20/0,1* 10/5]½ = 20 rad/s.

retour -menu