|
concours d'entrée médecine lentilles sphériques accolées, oscillateur élastique . Casablanca 2003 |
|||
|
|||
|
Données : g= 10 m/s² ; 10½ = 3,16 ; ln2 = 0,69.
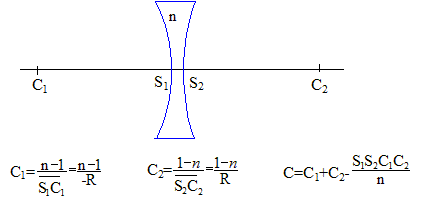
Donner la nature de l'objet. OA étant positif, l'objet se trouve à droite de la lentille ( au delà de la sortie du système optique) : objet virtuel. Calculer la distance focale de la lentille. Ecrire la formule de conjugaison avec OA= +0,03 m ; OA' = + 0,04 m. 1/OF' = 1/ OA - 1/ OA = 1/0,04-1/0,03 = (0,03-0,04) / (0,03*0,04) = -1/0,12 ; OF' =-0,12 m. Calculer la puissance ( vergence) de la lentille. C=1/OF' =-1/0,12 = -8,3 dioptries. La lentille est constituée de 2 portions de sphère de rayons R1=R2=R. Calculer R ( indice n=1,5). S1S2 étant faible devant R : C= C1+C2 = 2(1-n)/ R. R= 2(1-n)/C avcec 1/C=-0,12 ; R= 2(1-1,5)*(-0,12) ; R= 0,12 m. On accole une deuxième lentille à la première, l'image A"B" se forme à l'infini. Calculer la distance focale de la seconde lentille. L'image A'B' joue le rôle d'objet pour la seconde lentille : Ecrire la formule de conjugaison pour la seconde lentille avec 1/OA"=0.( image à l'infini ) 1/OF'2 = -1/OA'= -1/0,04 ; OF'2 = -0,04 m. Quelle est la nature de la seconde lentille ? OF'2 <0 , la seconde lentille est divergente. Calculer la distance focale de l'ensemble des deux lentilles. Les vergences des lentilles accolées s'ajoutent C= -8,3 + (-1/0,04 ) =-33,3 dioptries. Distance focale de l'ensemble : 1/(-33,3) = -0,03 m.
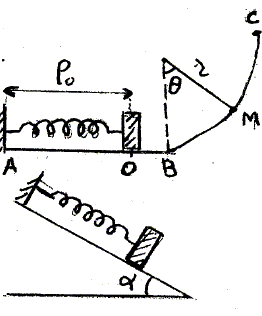
Un corps de masse m= 100 g est accroché à un ressort à spires non jointives de constante de raideur k= 100 N/m, de masse néglogeable et de longueur à l'équilibre L0= 20 cm. On comprime le ressort à une longueur L1= 12 cm. A l'instant t=0, on relâche le ressort sans vitesse initiale. Calculer l'énergie cinétique du corps m. L'énergie cinétique initiale est nulle. Calculer l'énergie potentielle du ressort. ½k(L0-L1)2 = 0,5*100 ( 0,2-0,12)2 =0,32 J. Calculer la vitesse lorsqu'il passe par O. En O, position d'équilibre, l'énergie mécanique est sous forme cinétique : ½mv2 = 0,32 ; v2 = 2*0,32 / m
= 0,64 / 0,1 = 6,4 = 2,5
m/s. T= 2p (m/k)½ =2p (10-3)½ =0,20 s. Donner l'équation horaire du mouvement. x(t) = (L0-L1) cos ( 2pt/T + j) ; (L0-L1) =0,08 m ; 2p/T = (103)½ =31,6 rad/s. A t=0, x(0) = -0,08 m d'où : -0,08 = 0,08 cos j ; cos j =-1 ; j = p. x(t) = 0,08 cos ( 31,6 t + p)
Le corps se déplace sans frottement sur un rail constitué par une portion de droite AB et une portion de cercle BC de rayon r=40 cm. A un instant donné lors de son passage par le point O le corps est libéré, et s'arrête au point M.
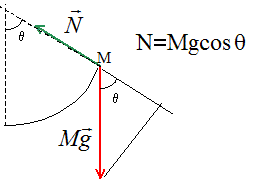
Calculer l'angle q. En O, l'énergie mécanique du corps est sous forme cinétique et vaut 0,32 J. En M l'énergie mécanique est sous forme d'énergie potentielle de pesanteur. On choisit comme origine de l'énergie potentielle de pesanteur le point B ; l'altitude du point M est alors : r(1-cos q). L'énergie potentielle de pesanteur en M vaut : mgr(1-cos q) =0,1*10*0,4 (1-cos q) = 0,4 (1-cos q). L'énergie mécanique se conserve : 0,32=0,4(1-cos q) ; 1-cos q = 0,8 ; cos q =0,2 ; q = 78°. Calculer la réaction du rail en M.
N= 0,1*10 *cos78 = 0,2 N.
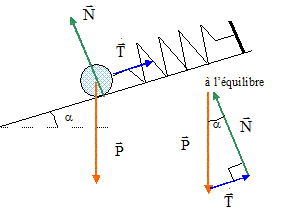
Le même ressort avec le corps est placé sur un plan incliné ( a=30°). La masse glisse sans frottement. Calculer l'élongation du ressort.
T= mg sin a = 0,1*10*0,5 = 0,5 N de plus T= k (L-L0 ) ; L-L0= T/k = 0,5/100 = 0,005 m ; L-L0= 5 mm. On tire la masse m de sa position d'équilibre d'une distance xm= 4 cm, puis on la libère sans vitesse initiale. On considère l'instant t=0 lors du premier passage par la position d'équilibre. Calculer la période d'oscillation du ressort. T= 2p (m/k)½ =2p (10-3)½ =0,20 s. Donner l'équation horaire du mouvement. x(t) = xm cos ( 2pt/T + j) ; xm =0,04 m ; 2p/T = (103)½ =31,6 rad/s. A t=0, x(0) = 0 d'où : 0 = 0,04 cos j ; cos j =0 ; j =½ p. x(t) = 0,04 cos ( 31,6 t + ½p)
|
|||
|
|