Machine frigorifique concours ITPE 2007

On suppose dans un premier temps que le cycle comprend les transformations réversibles suivantes : compression adiabatique de T₂ à T₁ , compression isotherme à T₁ , détente adiabatique de T₁ à T₂, détente isotherme à T₂.

Tracer l'allure du cycle dans un diagramme (P V).

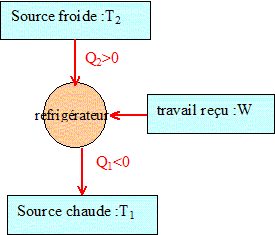
 Justifier rapidement que l'on a Q₁<0 et Q₂>0.

Au cours d'un cycle le fluide reçoit le travail W , prend la chaleur Q₂ à la source froide (aliments à refroidir) et céde la chaleur Q₁ à l'extérieur, source chaude.

Q₂ reçue par le fluide est comptée positivement.

Q₁ cédée par le fluide est comptée négativement.

Définir et calculer l'efficacité h du cycle.

coefficient d’efficacité , notée h, ( réversibilité) : chaleur enlevée à la source froide divisée par le travail reçu.

h = Q₂/W.

premier principe : W+Q₁+Q₂ = 0 sur le cycle d'où W= -(Q₁+Q₂)

h = -Q₂/(Q₁+Q₂).

second principe : Q₁/T₁+Q₂/T₂ <= 0 sur le cycle.

Q₁/T₁ <= -Q₂/T₂ ; Q₁/Q₂<= -T₁/T₂ ; (Q₁+Q₂) /Q₂<= (T₂-T₁) /T₂ ;

d'où : -Q₂/ (Q₁+Q₂) <= T₂/(T₁-T₂)

( égalité pour une transformation réversible ; inférieur dans le cas d'une transformation irréversible )

 h = T₂/(T₁-T₂).

h =268/(293-268) =10,7.

En réalité le cycle comprend les transformations suivantes :

- compression adiabatique réversible de T₂ à T'₂ = 330 K

- refroidissement isobare de T'₂ à T₁ .

- détente adiabatique réversible de T₁ à T'₁

- échauffement isobare de T'₁ à T₂ .

Exprimer l'efficacité h' du cycle en fonction de T₁, T'₁, T₂, T'₂.

Compression adiabatique réversible de T₂ à T'₂ :

Q₁=0 ; dW = -PdV avec PV^g=Cte ; dW =-Cte V^-g dV

W= -Cte / (1-g) (V^1-g_final-V^1-g_initial)

Or Cte = P_initialV^g_initial= P_finalV^g_final

d'où : W= 1/ (g-1) [ P_finalV_final - P_initialV_initia] = R/ (g-1) [T_final-T_initial]

W₁ = R/ (g-1)[T '₂-T₂].

Détente adiabatique réversible de T₁ à T'₁ :

Q₃=0 ; W₃ = R/ (g-1)[T '₁-T₁].

Refroidissement isobare de T'₂ à T₁ :

dW = -PdV avec P constant. W = -P(V_final-V_initial) = R(T_initial-T_final)

W₂ = R[T '₂-T₁].

Q = C_p(T_final-T_initial) = gR/(g-1)(T_final-T_initial)

Q₂ = gR/(g-1)(T₁-T '₂).

Echauffement isobare de T'₁ à T₂ :

W₄ = R[T '₁-T₂]. Q₄ = gR/(g-1)(T₂-T '₁).

W =R [ 1/(g-1) (T '₂-T₂+T '₁-T₁) + (T '₂-T₁ +T '₁-T₂ ]

W = Rg/(g-1)(T '₂-T₂+T '₁-T₁)

h' = Q₄/W.

h' = (T₂-T '₁) / (T '₂-T₂+T '₁-T₁).

Exprimer l'efficacité h' du cycle en fonction de T₂, T'₂.

Compression adiabatique réversible de A à B :

 P_A V_A^g =  P_B V_B^g (1)

Refroidissement isobare de B à C :

P_B V_B = RT '₂ et P_B V_C = RT₁(2)

Détente adiabatique réversible de C à D :

 P_B V_C^g =  P_A V_D^g (3)

Echauffement isobare de D à A :

P_A V_D = RT'₁ et P_AV_A = RT₂(4)

(1) et (3) donnent : V_A^g /V_D^g = V_B^g / V_C^g soit V_A /V_D = V_B / V_C (5)

(2) donne : T '₂ / V_B = T₁/ V_C ; V_B / V_C = T '₂ / T₁ (6)

(4) donne : T '₁ / V_D = T₂/ V_A ; V_A / V_D = T₂ / T '₁ (7)

(5), (6) et (7) donnent : T '₁ = T₁ T₂/ T '₂ .

Repport dans h'.

h'= (T₂-T '₁) / (T '₂-T₂+T '₁-T₁).

h'= (T₂T '₂-T₁ T₂) / (T '₂T '₂-T₂T '₂+T₁ T₂-T₁T '₂).

h'=T₂(T '₂-T₁ ) / [(T '₂-T₁ ) (-T₂ +T '₂).

h'=T₂ /( T '₂-T₂)

h'=268/(330-268 = 4,3.

 Calculer la variation d'entropie de l'ensemble fluide-sources au cours du cycle pour une mole de fluide.

 L'entropie est une fonction d'état : sa variation ne dépend que de l'état initial et final.

imaginer une transformation réversible passant de l'état initial à l'état final

transformation élémentaire : dS =dQ/T= (dU-dW)/T = C_{v, m} /T dT+ PdV/T = R/(g-1) /T dT+ RdV/P

intégrer entre T_i et T_f : DS =R/(g-1) ln(T_f /T_i) + Rln(V_f /V_i).

Refroidissement isobare de T'₂ à T₁ (B à C)

DS_BC =R/(g-1) ln(T₁ /T '₂) + Rln(V_C /V_B).

Or V_B / V_C = T '₂ / T₁ (6)

DS _BC =R/(g-1) ln(T₁ /T '₂) + Rln(T₁ /T '₂) = Rg/(g-1) ln(T₁ /T '₂)

DS_DA =R/(g-1) ln(T₂ /T '₁) + Rln(V_A /V_D).

Or V_A / V_D = T₂ / T '₁ (7)

DS _DA =R/(g-1) ln(T₂ /T '₁) + Rln(T₂ /T '₁) = Rg/(g-1) ln(T₂ /T '₁)