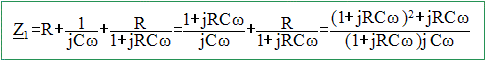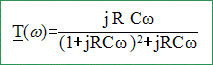Fonction de transfert, diagramme de Bode concours ITPE 2007

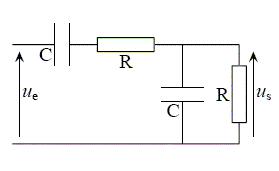
Déterminer la fonction de transfert T(w) = U_s/U_e.

admittance complexe de R et C en parallèle :

Y = 1/R + jCw.

impédance complexe : Z =1/Y =1/(1/R+jCw) = R/(1+jRCw).

impédance complexe de l'ensemble :

Z₁ = R+1/(jCw) + Z .

U_s/U_e=Z / Z₁

1 -(RCw)²+3jRCw

Multiplier numérateur et dénominateur par l'expression conjuguée : 1 -(RCw)² -3jRCw

Le dénominateur s'écrit : D= [1 -(RCw)²]² + 9(RCw)² = 1+7(RCw)² +(RCw)⁴.

Le numérateur s'écrit :

N=jR²Cw [1 -(RCw)² -3jRCw]= 3(RCw)²+ [1 -(RCw)²] jRCw.

Etablir à partir de T(w), l'équation différentielle reliant u_s(t) à u_e(t).

La multiplication par jw est associée à la dérivée première par rapport au temps.

La multiplication par(jw)² = -w² est associée à la dérivée seconde par rapport au temps.

N= -3R²C² (-w² ) + [1 -(RCw)²] R C jw.

u_s(t) =1/D [ -3R²C² u_e"(t) + (1 -(RCw)²) RC u_e'(t) ]

Calculer la phase j. tan j = [1 -(RCw)2] R C w / [3(RCw)2] tan j =[1 -(RCw)2] / (3RCw).

Calculer le gain T.

N = 3(RCw)²+ [1 -(RCw)²] jRCw.

norme de N : N² = 9(RCw)⁴ +[1 -(RCw)²]² (RCw)²

N² = 9(RCw)⁴ +[1 -2(RCw)²+(RCw)⁴] (RCw)²

N² = 9(RCw)⁴ +(RCw)² -2(RCw)⁴+(RCw)⁶

N² = (RCw)² [1 +7(RCw)²+(RCw)⁴ ]

N= RCw[1 +7(RCw)²+(RCw)⁴ ]^½.

Or D = 1+7(RCw)² +(RCw)⁴.

T= N/D = RCw [1 +7(RCw)²+(RCw)⁴ ]^-½.

Déterminer le maximum T_max de T et la fréquence f₀ correspondante.

Dériver T par rapport à w :  On pose x = RCw

T = x [1 +7x ²+x⁴ ]^-½.

x= ; x' = 1 

v = [1 +7x ²+x⁴ ]^-½ ; v'=-0,5 [14x+4x³ ][1 +7x ²+x⁴ ]^-3/2.

T ' = [1 +7x ²+x⁴ ]^-½ -0,5x [14x+4x³ ][1 +7x ²+x⁴ ]^-3/2.

T ' = [1 +7x ²+x⁴ ] ^-3/2 {[1 +7x ²+x⁴ ] -0,5x [14x+4x³ ] }

T ' = 0 si : 1 +7x ²+x⁴=7x ²+2x⁴

x⁴ = 1 ; x = x₀ = 1 ; RCw₀ = 1 ; w₀ =1/(RC).

Or w₀ =2pf₀ ; f₀ = 1/(2pRC).

T _max = [1 +7+1 ]^-½ = 1/3.

Il s'agit bien d'un maximum car lorsque x tend vers zéro ou l'infini, T tend vers zéro.

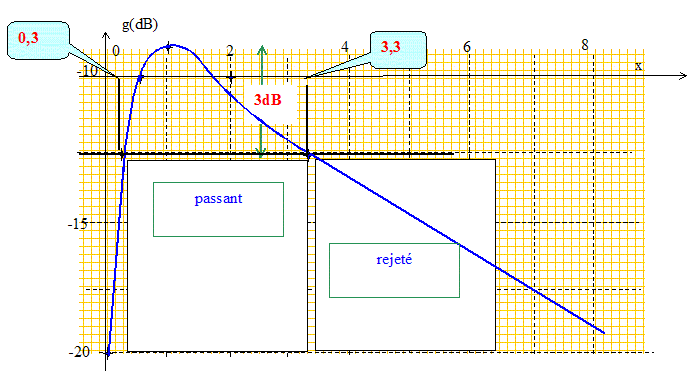
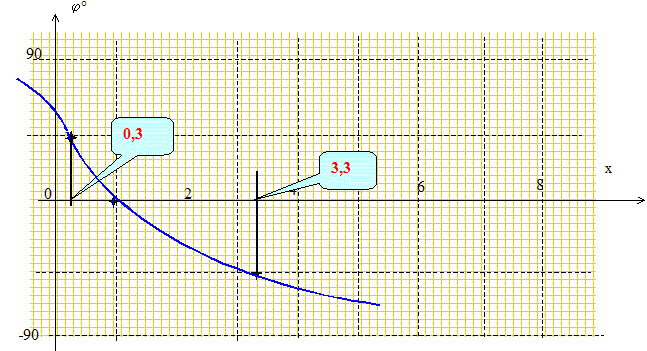
Calculer les fréquences de coupure et la largeur de la bande passante.

 Les fréquences de coupures ( à 3 dB) sont telles que : T = T_max / 2^½ ou T² = ½ T²_max = 1/18.

soit T²= x² [1 +7x ²+x⁴ ]^-1 = 1/18

18x² = 1 +7x ²+x⁴ ; 1-11x ²+x⁴=0

Changement de variable : X= x² ; 1-11X + X²=0

D =121-4 = 117 ; D^½ =10,816

X₁ = (11-10,816) /2 = 0,0916 ; X₂ = (11+10,816) /2 = 10,908.

x₁ =3,30 ; x₂ =0,30.

f₁ = 3,30 f₀ ; f₂ = 0,30 f₀ ; Df =f₁- f₂ = 3 f₀.

Tracer le diagramme de Bode en gain, en phase.

T = [1/x² +7+ x² ]^-½.

Il faut représenter la fonction : g(dB) = 20 log T = -10 log (1/x² +7+x²)

x	0,1	0,3	0,5	1	2	3,3	4	5	10
g(dB)	-20,9	-12,6	-10,5	-9,5	-10,5	-12,6	-13,6	-15	-20,3
j(°)	73	45	28	0	-28	-45	-51	-58	-73