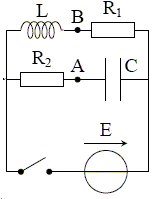
Dipôle RLC, montage en parallèle concours ITPE 2007

Au début de l'expérience, on laisse le circuit assez longtemps avec l'interrupteur ouvert. A t=0, on ferme l'interrupteur.

Que peut-on dire de l'état du circuit ( bobine et condensateur ) juste avant la fermeture de l'interrupteur. Justifier.

Le condensateur est déchargé ( tension nulle à ces bornes).

La bobine ne stocke aucune énergie : l'intensité du courant est nulle. 

Lors des échanges d'énergie entre condensateur et bobine, l'énergie stockée par le condensateur et la bobine est dissipée par effet joule dans les résistors R₁ et R₂.

Déterminer l'intensité i(t) du courant qui traverse le générateur.

On note avec l'indice 1 l'intensité qui traverse la branche contenant la bobine, avec l'indice 2 celle qui traverse la branche contenant le condensateur, i celle traversant le générateur.

Additivité des intensités : i = i₁ + i₂.

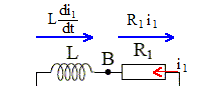
additivité des tensions : E= Ldi₁/dt + R₁i₁. 

di₁/dt + R₁/L i₁ =E/L ; on pose t₁ = L/R₁.

di₁/dt +1/t₁ i₁ =E/L. (1)

solution de cette équation différentielle sans second membre : i₁ = A exp(-t/t₁ )

solution particulière de (1), régime permanent : I₁ = E/R₁.

solution générale de (1) : i₁ = A exp(-t/t₁ ) + E/R₁.

Condition initiale i₁ = 0 d'où : 0 =A +E/R₁ ; A = -E/R₁.

i₁ = E/R₁ ( 1-exp(-t/t₁ ).

i2 = dq/dt.

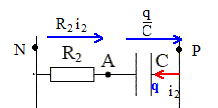
additivité des tensions : E= q/C + R₂i₂. 

E= q/C + R₂dq/dt. 

q/(R₂C) + dq/dt = E/ R₂ ; on pose t₂ = R₂C

q/ t₂ + dq/dt = E/ R₂ (2)

solution de cette équation différentielle sans second membre : q = B exp(-t/t₂ )

solution particulière de (2), régime permanent, condensateur chargé : Q = CE.

solution générale de (21) : q = B exp(-t/t₂) + CE.

Condition initialeq = 0 d'où : 0 =B +CE ; B = -CE.

q = CE ( 1-exp(-t/t₂ ).

Or i₂ = dq/dt d'où i₂ = CE/t₂ exp(-t/t₂)

i₂ = E/ R₂ exp(-t/t₂).

i = i₁+i₂ = E/R₁ ( 1-exp(-t/t₁ ) +E/ R₂ exp(-t/t₂).

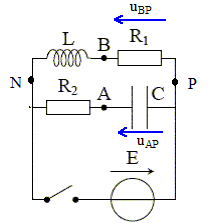
A quelle condition cette intensité est-elle indépendante du temps ?

En régime permanent l'intensité est indépendante du temps et vaut I= E/R₁.

En régime transitoire :

E/R₁ exp(-t/t₁ ) =E/ R₂ exp(-t/t₂)

R₂/R₁ = exp(-t/t₂) exp(t/t₁ )

ln( R₂/R₁ )= -t/t₂+t/t₁ = t (1/t₁ -1/t₂)

soit à la date t = ln( R₂/R₁ ) / (1/t₁ -1/t₂)

A quelle condition la tension u(t) = V_A(t) - V_B(t) est-elle nulle en permanence ?

u(t) = u_AB =  u_AP+ u_PB.

u(t) = -q/C +R₁i₁ =0

q/C = R₁i₁

R₁  i₁ = E ( 1-exp(-t/t₁ ) ; q /C=E ( 1-exp(-t/t₂ ).

1-exp(-t/t₁ ) = 1-exp(-t/t₂ ) ; exp(-t/t₂ ) ; t/t₁ =t/t₂.

t₁ =t₂ ; L/R₁ = R₂C.