Lentilles ; cercle oculaire ; profondeur de champ concours ITPE 2007

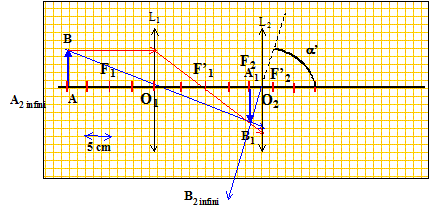
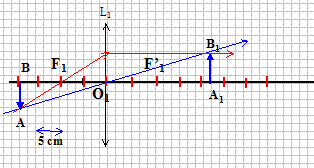
Un viseur est constitué d'un objectif L₁ ( lentille convergente de distance focale f'₁= 10 cm, diamètre d₁=3,0 cm ) et d'un oculaire L₂ ( lentille convergente de distance focale f'₂ = 2,0 cm). Il est réglé de façon à viser à 20 cm de la face d'entrée de l'objectif ( c'est à dire que l'oeil regardant à travers le viseur voit nettement et sans accomoder les objets situés dans le plan de front situés à 20 cm devant L₁).

Déterminer la distance L entre les deux lentilles.

L'objectif L₁ donne de l'objet AB une image "intermédiaire " A₁B₁  ; cette image sert d'objet pour l'oculaire L₂ : l'image définitive est notée A₂B₂.

L'oeil voit nettement sans accommoder :

- l'image définitive A₂B₂ est à l'infini.

- A₁B₁ est dans le plan focal objet de L₂.

On écrit en bleu et en gras les distances algébriques.

Appliquer la formule de conjugaison à la lentille L₁.

1/O₁F'₁ = 1/O₁A₁ - 1/O₁A.

1/O₁A₁ = 1/f'₁ + 1/O₁A = 1/0,1 + 1/(-0,2) = 10-5 = 5 ; O₁A₁ = 1/5 = 0,2 m = 20 cm.

distance des deux lentilles :

L=O₁A₁ +A₁O₂ = O₁A₁ +F₂O₂ = 20 + 2,0 = 22 cm.

Déterminer la position et le diamètre du cercle oculaire, c'est à dire l'image de l'objectif donnée par l'oculaire.

Appliquer la formule de conjugaison à la lentille L₂. L'objet est la lentille L₁.

1/O₂F'₂ = 1/O₂A' - 1/O₂O₁.

1/O₂A' = 1/f'₂ + 1/O₂O₁ = 1/0,02 + 1/(-0,22) = 50-4,545 = 45,45 ; O₂A' = 1/45,45 = 0,022 m = 2,2 cm.

Position du cercle oculaire : 2,2 cm à droite de L₂.

Grandissement transversal : g = O₂A' / O₂O₁ = 2,2 / (-22) = -0,1.

diamètre du cercle oculaire : 0,1 d₁ = 0,1*3 = 0,3 cm = 3 mm.

Calculer le rapport P= a' / AB.

Dans le triangle O₂A₁B₁ : tan a' =  A₁B₁ / f'₂.

grandissement transversal ( lentille L₁ ) : |g | = A₁B₁ /AB = O₁A₁/O₁A = 22/20 = 1,1

A₁B₁ = |g | AB.

tan a'=  |g | AB / f'₂ ; tan a' / AB = |g |/ f'₂

tan a' / AB=1,1 /0,02 = 55.

si a' est petit, alors tan a' voisin de a' radian.

La profondeur de champ est la région de l'espace objet que l'observateur peut voir en accommodant à travers le viseur.

Déterminer la profondeur de champ dans les deux cas suivants :

On suppose l'oeil placé dans le plan focal image de L₂.

L'oeil accomode au maximum : l'image définitive virtuelle A₂B₂ est à 12,5 cm à gauche de F'₂.

O₂A₂ = -(12,5-2 =) = -10,5 cm = -0,105 m.

Appliquer la formule de conjugaison à la lentille L₂.

1/O₂F'₂ = 1/O₂A₂ - 1/O₂A₁.

1/O₂A₁ = 1/O₂A₂-1/f'₂ = 1/(-0,105) - 1/0,02 = -9,52-50 = -59,52 ; O₂A₁ = -1/59,52 =-0,0168 m = -1,7 cm.

O₁A₁ = O₁O₂ +O₂ A₁=22-1,68 =20,32 cm = 0,203 m.

Appliquer la formule de conjugaison à la lentille L₁.

1/O₁F'₁ = 1/O₁A₁ - 1/O₁A.

1/O₁A = 1/O₁A₁-1/f'₁ = 1/0,203- 1/0,1 =4,92-10 = -5,08 ; O₁A = -1/5,08 =-0,197 m = -19,7 cm.

La profondeur de champ est la distance, mesurée sur l'axe optique, qui sépare les positions extrêmes de l'objet pour lesquelles on peut considérer que l'image qui se forme sur un écran fixe ( l'oeil ) est nette.

Donc région comprise entre 20 cm et 19,7 cm à gauche de L₁.

On suppose l'oeil placé contre la lentille L₂.

Même calcul que ci-dessus.

L'oeil accomode au maximum : l'image définitive virtuelle A₂B₂ est à 12,5 cm à gauche de F'₂.

O₂A₂ = -12,5 cm = -0,125 m.

Appliquer la formule de conjugaison à la lentille L₂.

1/O₂F'₂ = 1/O₂A₂ - 1/O₂A₁.

1/O₂A₁ = 1/O₂A₂-1/f'₂ = 1/(-0,125) - 1/0,02 = -8-50 = -58 ; O₂A₁ = -1/58 =-0,01724 m = -1,72 cm.

Appliquer la formule de conjugaison à la lentille L₁.

1/O₁F'₁ = 1/O₁A₁ - 1/O₁A.

1/O₁A = 1/O₁A₁-1/f'₁ = 1/0,2028- 1/0,1 =4,932-10 = -5,068 ; O₁A = -1/5,068 =-0,1973 m = -19,7 cm.