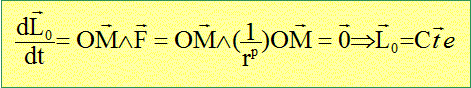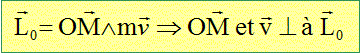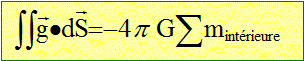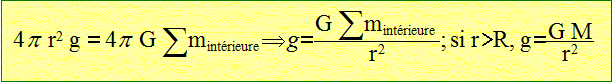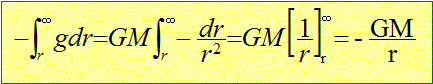|
Etude d'un satallite dans le champ gravitationnel terrestre concours ITPE 2006 |
||||
|
||||
|
Qu'appelle t-on interaction newtonienne ? Donner deux exemples. L'interaction de type newtonienne s'exprime sous la forme k/r2. ( k est une constante) Gravitation ( attractive) k = -GMm Electrostatique ( Coulomb) : attractive ou répulsive : k= q1q2 / (4pe0). Les forces newtoniennes sont des forces centrales. Préciser ce terme. Citer des forces centrales qui ne sont pas newtoniennes. La direction de la force passe par un point unique O. La force est indépendante du temps. La force ne dépend que de la distance r=OM. La force linéaire de Hooke est " centrale", non "newtonienne" :
Les forces proportionnele à rp sont centrales, non newtoniennes. On considère un point matériel M de masse m, soumis à une force centrale. Montrer que le moment cinétique L0 de la particule M par rapport au centre de force O est constant dans le temps. Conclure. Théorème du moment cinétique en O.
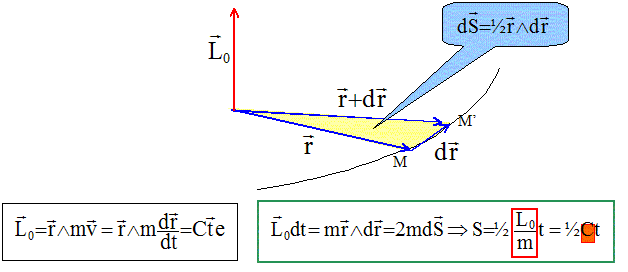
Le moment cinétique étant un vecteur constant, la trajectoire est plane, contenue dans un plan perpendiculaire au vecteur moment cinétique. Qu'appelle t-on "loi des aires". C= L0/m est
la constante des aires. La trajectoire est
parcourue suivant la loi des
aires. Dans
un mouvementà force centrale, le rayon
vecteur balaie des aires égales pendant des
durées
égales. On assimile la terre à une sphère homogène de centre O, de rayon R et de masse M. L'objet de l'étude est un satellite terrestre S, assimilable à un point matériel de masse m, soumis au champ gravitationnel terrestre. A quelle condition peut-on supposer que le mouvement du satellite peut s'étudier dans un référenteil galiléen lié à la Terre ? Un référentiel galiléen est un référentiel dans lequel un objet isolé est soit immobile, soit animé d'un mouvement rectiligne uniforme. Un référentiel terrestre est galiléen dans la mesure où l'expéreince est de courte durée. Le référentiel géocentrique ( solide formé par le centre de la terre et les centres d'étoiles lointaines qui semblent fixes) est commode pour l'étude des satellites de la terre. Ce référentiel est galiléen pour des durées inférieures à 1 jour ( on peut alors négliger la rotation de la terre autour du soleil). Par la suite on étudie S dans un référentiel galiléen lié à la terre. On utilise le repère cylindrique. On note r la distance OS et v le module de la vitesse de S dans ce référentiel. Utiliser le thèorème de Gauss pour calculer le champ gravitationnel terrestre en tout point de l'espace.
On choisit comme surface S est une sphère de rayon r : S = 4pr2.
Le vecteur champ de gravitation est dirigé vers O. En déduire le potentiel gravitationnel V associé. Le champ de gravitation dérive d'un potentiel scalaire V :( ce potentiel est nul à l'infini )
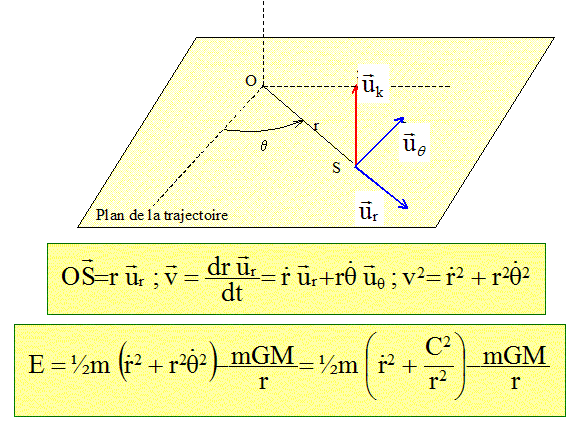
Expression de l'énergie mécanique du satellite. L'énergie mécanique E est la somme de l'énergie cinétique et de l'énergie potentielle.
avec C= r2q ' constante des aires.
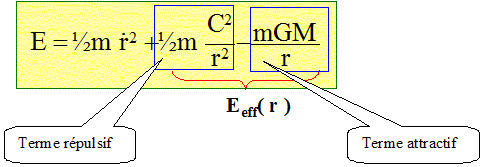
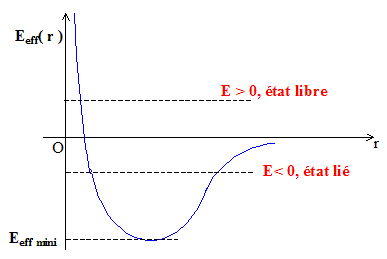
Le terme ½mr'² représente l'énergie cinétique d'une particule de masse m effectuant un mouvement suivant r : énergie cinétique radiale. Tracer l'allure de Eeff (r) en fonction de r.
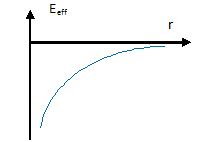
Les trajectoires associées à une interaction newtonienne sont des coniques. Préciser la nature de la conique-trajectoire en fonction du signe de E. On pose |E|=E0. E>0 et e >1 : hyperbole E=0 et e=1 : parabole -Eeff mini < E <0 et 0<e<1 : ellipse E= -Eeff mini : cercle E< -Eeff mini : mouvement impossible ; l'énergie initiale est insuffisante pour satelliser S. La trajectoire peut-elle être une droite ? Si oui, à quelle condition ? Tracer dans ce cas Eeff (r). Si la vitesse initiale v0 est dirigée vers le centre de la terre, la trajectoire est une droite. Eeff ne contient plus
que le terme attractif : -GmM / r ; la courbe est une
branche d'hyperbole.
On se place dans le cas d'une trajectoire liée. Exprimer le module v de la vitesse de S en fonction de E0 et r. A quelle condition la trajectoire est-elle un cercle ? E0 = ½mv2-GmM/r ; v = [2(E0/m +GM/r) ]½. La trajectoire est un cercle si Eeff est minimale. Dériver Eeff par rapport à r et chercher la valeur de r qui annule cette dérivée. Exprimer le rayon du cercle en fonction de la vitesse initiale v0 et des autres données. r = MG / v02. Calculer vl, appelée première vitesse cosmique, vitesse initiale de S dans le cas limite ou le rayon du cercle est RT. vl = (MG/RT)½ avec GM = g0R2T ; vl = (g0RT)½ = (9,8 *6,4 106)½ ~ 8 km /s. Qu'appelle t-on vitesse de libération vL pour le satellite S ? La calculer. Quelle est la trajectoire de S pour v0=VL ? C'est la vitesse initiale permettant au satellite se s'éloigner indéfiniment de la terre ( de se libérer de l'attraction terrestre) L'énergie du satellite, ( situé à l'infini) est nulle : ½mvL2-GmM/RT = 0 ; vL2 = 2GM/RT ; vL =2½vl ~ 11 km/s. pour v0=VL le satellite s'éloigne indéfiniment de la terre en décrivant un arc de parabole. Dans le cas où l'énergie mécanique de S est strictement positive, calculer vinf, vitesse de S "à l'infini". Quel est alors le mouvement de S ? Préciser qualitativement sur le graphe le domaine de r pour lequel le mouvement s'observe. Que vaut alors la force exercée par la terre sur S ? La force exercée par la terre sur le satellite à l'infini est nulle. L'énergie potentielle est nulle ( l'origine de cette énergie est prise à l'infini) ; E0 = ½mvinf2 ,
valeur positive, la trajectoire est une hyperbole.
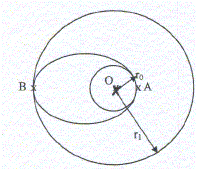
Sachant que E= - GmM/(2a) , calculer a, le demi grand-axe de l'ellipse-trajectoire en fonction de r0 et v0. A quelle condition sur v0, cette ellipse est-elle un cercle de rayon r0 ? E = -GMm/(2a) = ½mv02 - GmM/r0 ; 1/(2a) = -½ v02 /(GM) +1//r0 = (-½ v02r0 +GM) / (GMr0 ) ; 2a = GMr0 /(-½ v02r0 +GM). Si v02r0 = GM, l'éllipse est un cercle. Pour une trajectoire circulaire, établir une relation entre l'énergie cinétique et l'énergie potentielle de S. E =-GMm/(2r) = Ec + Ep = ½m v2 -GmM/r ; Ec = -GMm/(2r)+GmM/r = ½GMm/r ; Ec = -½Ep. Calculer le rayon de cette orbite pour que le satellite soit « géostationnaire», c'est-à-dire fixe pour un observateur immobile par rapport à la surface de la Terre. On rappelle que la Terre effectue une rotation sur elle-même en 24h. Ecrire la 3ème loi de kepler :T2/r3 = 4p2/(GM) ; r3 = GM T2/ (4p2) r = [ 6,67 10-11 * 6 1024 * (24*3600)2 / (4*3,142]1/3 = 4,2 107 m. L'altitude de l'orbite initiale atteignable par la navette n'est pas suffisante pour un satellite géostationnaire. L'orbite circulaire, de rayon r0, sur laquelle est lâché le satellite dans un premier temp sest appelée «orbite basse». Il Ifaut ensuite transférer le satellitesur une «orbite haute» caractériséepar OS=r1, r1 étant le rayon de l'orbite géostationnaire. Pour cela on utilise une trajectoire intermédiaire, elliptique, appelée« ellipse de transfert» de demi-grand axe 2a = r0 +rl.
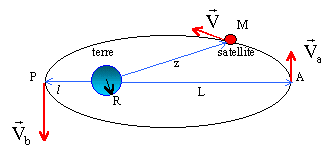
Sur la trajectoire elliptique, calculer les vitesses VA et VB du point S en A et B. Dessiner les vecteurs correspondants.
la force de gravitation est une force centrale, le moment cinétique se conserve en particulier en A et P : on note Za = R+L et Zp = R+ l ; m : masse du satellite m VaZa = mVpZp ; VaZa = VpZp ; Vp = VaZa / Zp. Le satellite est sur la trajectoire circulaire« basse» en A. A l'aide d'un moteur interne, on modifie par une brève impulsion sa vitesse et il passe sur la trajectoire elliptique. Quand il y est stabilisé, et qu'il passe en B, on modifie encore une fois sa vitesse par le même procédé afin qu'il se mette sur la trajectoire circulaire «haute ». En déduire la variation d'énergie à communiquer au satellite pour chaque étape, puis pour l'ensemble de la manoeuvre. Cette variation totale est-elle positive ou négative ? L'énergie mécanique sur la trajectoire elliptique se conserve aux points A et B : E = - GMm / (r1 +r0). énergie mécanique sur l'orbite circulaire basse au point A : E1 = -½ mGM / r0 variation d'énergie mécanique en A : DE = E -E1 = - GMm / (r1 +r0) + ½ mGM / r0 ; DE =GMm (r1 - r0) / [2(r1 +r0)r0]. DE est positive. Energie mécanique sur l'orbite circulaire haute : au point B : E2 = -½ mGM / r1 variation d'énergie mécanique en A : DE = E2 -E = - ½ mGM / r1 +GMm / (r1 +r0) ; DE =GMm (r1 - r0) / [2(r1 +r0)r1]. DE est positive. |
||||
|
|
||||
|
|
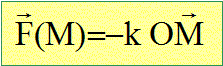k : raideur d'un ressort.
