optique : lentille concours ITPE ( travaux publics) interne 2006

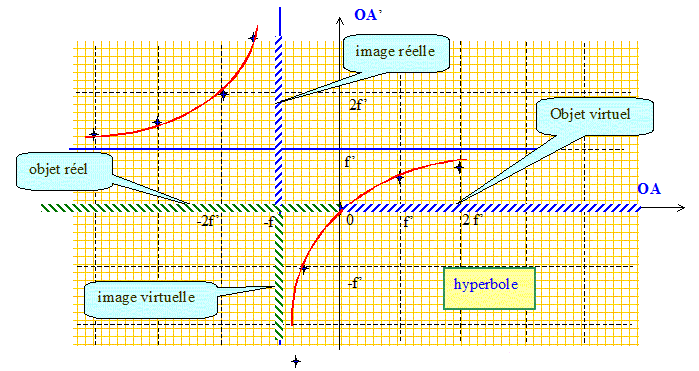
Soit une lentille mince convergente de centre O. On note F et F' ses foyers objet et image respectifs.

Préciser le signe de OF'.

Pour une lentille convergente la distance focale image OF' est positive ( F' à droite de O).

Donner la relation de conjugaison avec origine aux sommet pour un couple de points conjugués sur l'axe optique A et A'.

1/OF' = 1/OA' - 1/OA.

On cherche à traduire la relation de conjugaison par une courbe dans le plan ( OA ; OA' ) où l'abscisse est OA et l'ordonnée OA'.

Où se situe l'image d'un objet ponctuel placé au foyer principal objet F ?

1/OA = -1/OF'

La relation de conjugaison conduit à 1/OA' =0, c'est à dire une image rejetée à l'infini.

Où se situe l'image d'un objet ponctuel qui serait à l'infini sur l'axe ?

L'image d'un objet réel situé à l'infini sur l'axe se trouve au foyer principal image.

En déduire que le graphe que l'on recherche admet deux asymptotes que l'on caractérisera.

Tracer la relation de conjugaison. Quel type de courbe reconnaissez vous ?

Quelques valeurs : ( f' : distance focale image )

OA	-4f'	-3f'	-2f'	-1,5 f'	-0,75 f'	-0,5f'	-0,25 f'	f'	2f'
OA'	4f'/3	1,5 f'	2f'	3f'	-3f'	-f'	-f'/3	0,5 f'	2f'/3

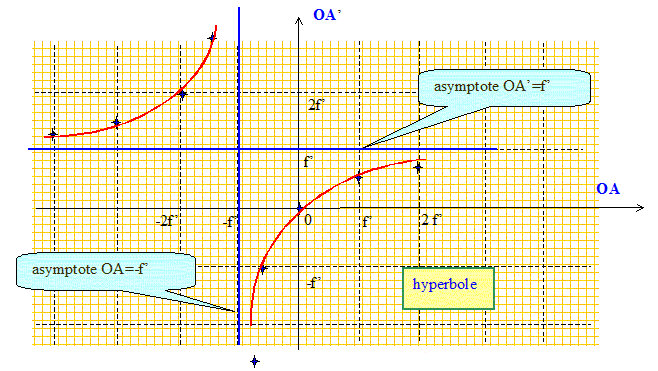
Repérer sur le graphe les zones où l'on a un objet réel. à gauche de la lentille : OA négatif Repérer sur le graphe les zones où l'on a un objetvirtuel. à droite de la lentille : OA positif

Repérer sur le graphe les zones où l'on a une image réelle.

à droite de la lentille : OA' positif

Repérer sur le graphe les zones où l'on a une image virtuelle.

à gauche de la lentille : OA' négatif

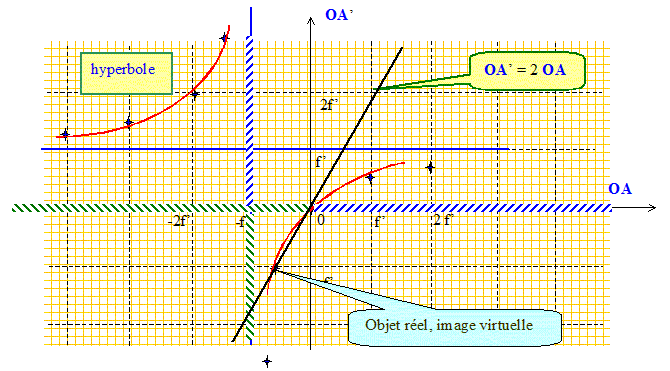
g= A'B'/AB = OA'/OA.

On fixe g = +2 :

tracer la relation correspondante sur le graphe précédent.

Lire les positions de l'objet et de l'image correspondantes.

OA'= 2 OA ; droite de coefficient directeur +2.

La relation de conjugaison s'écrit : 1/f' = 1/( 2 OA) - 1/OA = -1/( 2 OA) soit :

OA = -½f' et OA'= -f'.

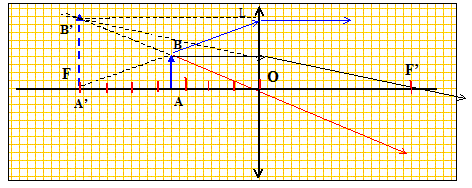
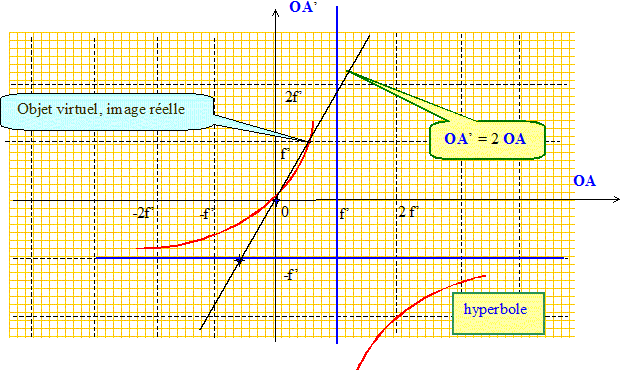
Rappeller les propriétés des rayons tracés.

Un rayon issu de B :

-passant par le centre optique O n'est pas dévié.

- parallèle à l'axe optique, émerge en passant par F'.

- passant par F, émerge parallèlement à l'axe optique.

La distance focale image d'une lentille divergente est négative.

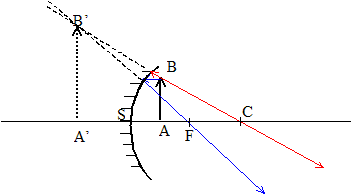
 Que devient ce graphique et l'étude précédente pour un miroir sphérique ?

On considère la relation de conjugaison avec origine au sommet et on se place dans le plan (SA ; SA')

miroir concave convergent

Caractéristiques de l'image A'B' d'un objet AB réel mesurant 1 cm, situé à 1 m du sommet, donnée par un miroir sphérique concave ( R=4 m)

calculs ( on écrit en bleu et en gras les distances algébriques) position :1/SA'-1/SA=-2/SC avec SC=-4 ; SA=-1 1/SA' =-2/SC +1/SA=-2/(-4)+1/(-1)=0,5-1 =-0,5 SA' = -2: image virtuelle située 2 m à gauche de S grandissement : g=SA' /SA=-2/-1 =+2 taille de l'image : 2 cm sens : le même que l'objet

construction un rayon (ou son prolongement), issu de B, passant par C, n'est pas dévié après réflexion. un rayon (ou son prolongement), issu de B, parallèle à l'axe optique, émerge après réflexion en passant par F