|
Un myope utilise une loupe concours ITPE ( travaux publics) interne 2004 |
||||
|
||||
|
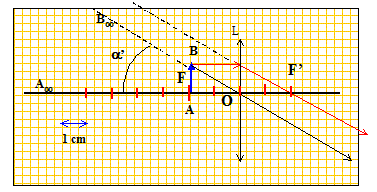
Utilisation normale de la loupe. L'utilisateur est jeune et possède une vue "normale", c'est à dire qu'il voit à l'infini sans accommoder ( oeil au repos) et jusqu'à la distance minimale Dm = 15 cm en accommodant au maximum. On définit le grossissement de la loupe par : G= a'/a. a' : angle sous lequel est vue l'image de l'objet observé au travers de la loupe. On suppose l'oeil placé directement derrière la loupe. a : angle sous lequel l'objet est vu à l'oeil nu à la distance Dm. Calculer G si l'observateur observe sans accomoder. L'image virtuelle étant à l'infini, l'objet se trouve au foyer objet F de la lentille.
tan a'=AB/f' voisin de a' si l'angle est petit. tan a = AB / Dm =AB/0,15 voisin de a si l'angle est petit G= Dm/f' = 0,15/0,02 = 7,5.
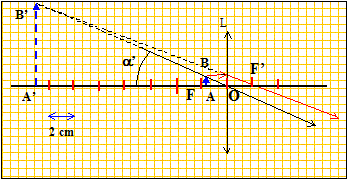
Calculer G' si l'observateur observe accomode au maximum. L'image virtuelle se trouve à la distance Dm=15 cm de la lentille.
tan a'=A'B'/A'O =A'B'/Dm voisin de a' si l'angle est petit. tan a = AB / Dm voisin de a si l'angle est petit. G' = A'B'/AB =OA'/OA = -Dm/OA. Calcul de OA ( formule de conjugaison ) 1/f' = 1/OA'-1/OA ; 1/OA = 1/OA'-1/f' 1/OA =1/(-0,15) - 1/0,02 = -(0,02+0,15) / (0,02*0,15) ; OA =-0,02*0,15/ 0,17 = -0,0176 m = -1,76 cm. G' = 0,15/0,0176 =8,5.
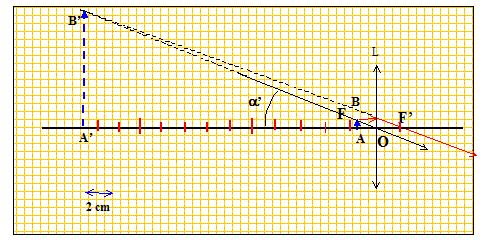
On considère un observateur jeune et myope ; son intervalle de vision nette est maintenant [25 ; 9,4 ] en cm. Calculer le grossissement G'' pour ce myope en supposant qu'il observe avec la loupe sans accommoder et sans lunette. L'image virtuelle se trouve à la distance D=25 cm de la lentille.
tan a'=A'B'/A'O =A'B'/D voisin de a' si l'angle est petit. tan a = AB / Dm = AB/0,094 voisin de a si l'angle est petit. G'' = A'B'/AB *Dm/D =OA'/OA *Dm/D = -D/OA *Dm/D = -Dm/OA. Calcul de OA ( formule de conjugaison ) 1/f' = 1/OA'-1/OA ; 1/OA = 1/OA'-1/f' 1/OA =1/(-0,25) - 1/0,02 = -(0,02+0,25) / (0,02*0,25) ; OA =-0,02*0,25/ 0,27 = -0,0185 m = -1,85 cm. G' = 0,25/0,0185 =13,5.
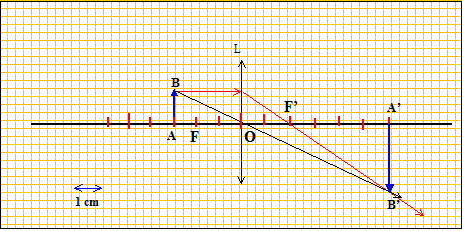
On utilise cette lentille pour projeter l'image d'un timbre rectangulaire ( fortement éclairé) de dimensions a x b. On obtient sur l'écran une image de taille 4(a x b). Calculer les positions de l'objet et de l'écran par rapport à la lentille.
La taille de l'image est 4 fois celle de l'objet : Chaque dimension du timbre a donc été multipliée par 2. Le grandissement g vaut donc -2. g = OA'/OA = -2 soit OA' = -2OA. Formule de conjugaison : 1/f' = 1/OA' - 1/OA 1/f' = 1/(-2OA)- 1/OA = -3/(2OA) ; OA = -1,5 f' = -3 cm ; OA' = -6 cm. |
||||
|
|
||||
|
|