|
ensemble de deux ressorts en rotation concours ITPE ( travaux publics) interne 2004 |
|||
|
|||
|
Un point matériel M de masse m est attaché aux extrémités de deux ressorts de même caractéristiques ( raideur k, longueur à vide l0), enfilés sur une tringle OA de longueur L et fixés respectivement en O et en A. On repère la position de M par x, distance OM. La tringle OA est fixe.
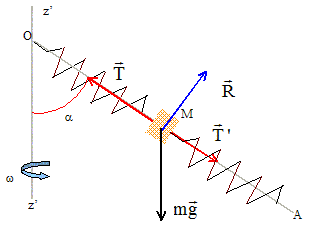
Position M0 du point M à l'équilibre : OM0 = x0. Le système étudié est le solide ponctuel M ; il est soumis à son poids, aux tensions des ressorts et à l'action de la tige OA. Les ressorts sont supposés être étirés.
Projetons chaque force sur OA, orienté de O vers A : poids : mg cos a ; action de la tige : 0 ; tension T' : k(L-x0-l0) ; tension T : -k(x0-l0) d'où : mg cos a + k(L-x0-l0) -k(x0-l0) =0 mg cos a +kL-2kx0 = 0 x0 = ½ [L+ mg cos a / k].
Le point M étant à l'équilibre, on l'écarte d'une amplitude xmax(>x0) et on le lâche sans vitesse initiale Ecrire la seconde loi de Newton sur l'axe OA, orienté de O vers A, origine M0 : On note la position M0M= x à une date t quelconque. poids : mg cos a ; action de la tige : 0 ; tension T' : k(L-x0-x-l0) ; tension T : -k(x0+x-l0) avec x>0. d'où : mg cos a + k(L-x0-x-l0) -k(x0+x-l0) =mx" mg cos a +kL-2kx0 -2kx = mx" Or mg cos a +kL-2kx0 =0 d'où mx"+ 2kx=0 x" +2k/m x =0. Expression de x(t) : Il s'agit d'un oscillateur non amorti de pulsation w0 =[2k/m]½. x(t) = xmax cos( w0t)
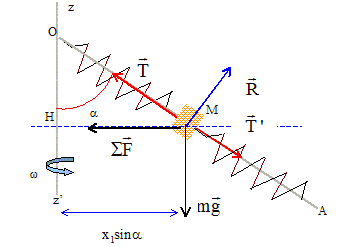
Nouvelle position d'équilibre x1 :
Projection de la somme vectorielle des forces sur un axe perpendiculaire à OA : R= mg sina. Le mouvement est circulaire uniforme de rayon MH = x1 sina ; l'accélération est centripète dirigée de M vers H. La valeur de l'accélération est : w2 MH = w2x1 sina. La seconde loi de Newton s'écrit suivant MH : -R cosa + Tsina - T'sina = m w2x1 sina. -mgcosa + T - T'= m w2x1. -mgcosa + k(x1-l0) - k(L-x1-l0)= m w2x1. -mgcosa + 2kx1-kL=m w2x1. x1 [ 2k-m w2]= mgcosa+kL x1 = ( mgcosa+kL) / [ 2k-m w2]. |
|||
|
|
|||
|
|