Aurélie 23/10/07
 

électricité : régime sinusoïdal concours ITPE ( travaux publics) interne 2003

Google

Un dipôle est alimenté en régime sinusoïdal par u(t) = Um cos (wt) avec Ue = 220 V et f=50 Hz. L'intensité du courant est alors :

i(t)=Im cos (wt+F)

Déterminer l'impédance complexe du dipôle et son module Z.

A u(t) on associe le nombre complexe u = Um ( nombre réel)

A i(t) on associe le nombre complexe i = Im exp(jF).

L'impédance complexe z est égale à : z = u / i =Um / Im exp(-jF).

module de z : Z=Um / Im

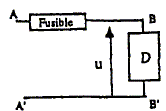
Déterminer la puissance électrique moyenne P absorbée par ce dipôle.

P =Ue Ie cos(F).

En déduire l'expression P= R(Ue/Z)2, R étant la résistance du dipôle.

cos F = R / Z ; Ie = Ue/ Z.

Par suite P= Ue Ue/ Z R / Z = R(Ue/Z)2.

Un fusible protège une ligne électrique [AB, A'B'], alimentant en régime sinusoïdal sous la tension efficace Ue = 220 V et la fréquence f= 50 Hz un dipôle D assimilable à une bobine d'inductance L=30 mH en série avec un résistor R. L'intensité efficace maximale admissible dans la ligne est 16 A.

Ce dipôle absorbe une puissance moyenne P= 2,5 kW. La ligne se comporte comme un conducteur ohmique de résistance totale R0 = 1,2 W fusible compris.
Calculer les deux valeurs possibles de la résistance R.

Impédance Z du dipôle : Z2 = R2 + (Lw)2 avec w = 2pf = 2*3,14*50 = 314 rad/s.

D'autre part Z = Ue/Ie.

L'intensité efficace maximale vaut 16 A d'où la valeur minimale de Z :

Zmini = 220/16 = 13,75 W.

Valeur minimale de R :

R2 = Z2 -(Lw)2 =13,752-(0,03*314)2 = 100 ; Rmini = 10 W.

L'autre solution R= -10 ohms n'est pas à retenir.

Autre méthode :

Seul le résistor absorbe de la puissance : 2500 = RI2 d'où R = 2500/162 = 9,8 W.

En déduire les intensités efficaces dans le dipôle.

Le dipôle est traversé par le courant de ligne soit Ie=16 A.

En déduire la puissance P0 dissipée par effet joule dans cette ligne.

P0 = R0Ie2 = 1,2*162 = 307 W.
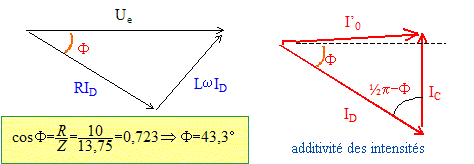
On ajoute, en parallèle sur le dipôle D un condensateur de capacité C=130,4 mF.

Calculer les intensités efficaces, Id dans le dipôle, IC dans le condensateur et I'0 dans la ligne.

Id = Ue/ZD = 220/13,75 = 16 A

Impédance du condensateur : ZC= 1/(Cw) ; IC= Ue/ZC = UeCw

IC =220*130,4 10-6*314 = 9,0 A

 

I'02 = IC2+Id2-2ICId cos (90-43,3)

I'02 = 92+162-2*16*9 cos 46,7 = 139 ; I'0 = 11,8 A.

Cette valeur étant inférieure à 16 A, le fusible ne fond pas.

Calculer la puissance P'0 dissipée dans la ligne par effet Joule.

P'0 = R0I'02 = 1,2*11,82 =167 W.

retour -menu