Satellite : période, énergie mécanique concours ITPE ( travaux publics) interne 2003

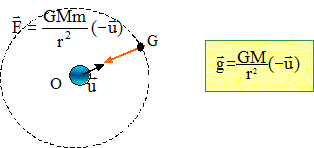
Pour un point P, le champ gravitationnel terrestre est , avec CP et r > R.

La valeur de ce champ au sol est g₀ = 10 m/s².

On donne R= 6400 km ; masse du satellite m = 20 kg ; altitude du satellite z = 12,8 km.

Calculer l'énergie nécessaire pour amener la masse m de l'altitude zéro jusqu'à l'altitude z.

La vitesse initiale et la vitesse finale sont supposées nulles.

L'énergie à mettre en oeuvre est égale à l'opposée du travail du poids.

E= m g z.

E = 20 * 10 * 12,8 10³ = 2,56 10⁶ J.

Ecrire la troisième loi de Kepler

T² / r³ = 4p²/(GM) = 4p²/(g₀R²).

avec r = R+z = 6400+12,8 = 6412,8 km = 6,4128 10⁶ m.

R= 6,4 10⁶m ; g₀ = 10 m/s².

T² = r³ 4p²/(g₀R²) ; T = 2p/R (r³/g₀)^½.

T= 2*3,14/6,4 10⁶ (( 6,4128 10⁶)³ / 10)^½ =5,04 10³ s.

Calculer l'énergie mécanique de ce satellite. EM = -GMm/(2r)= -g0R2m/(2r). EM= -20*10 (6,4 106)2 /(2* 6,4128 106) EM= -6,38 108 J.

Le même satellite sera considéré sur une orbite circulaire rasante autour de la terre, puis autour de la lune.

Démontrer que la période de révolution d'un tel satellite ne dépend que de la masse volumique de la planète.

 T² / r³ = 4p²/(GM)

T² = 4p²r³/(GM) (1)

masse (kg) = masse volumique ( kg m^-3) * volume (m³)

M = r 4/3p r³ avec r voisin de R

4pr³ /M= 3/r.

Repport dans (1) : T² =3p/(Gr)

T= [3p/(Gr)]^½.

Calculer la masse volumique r de la terre. G= 6,67 10^-11 SI

 r=3p/(GT²) avec T = 5,04 10³ s ; T² = 2,54 10⁷.

r=3*3,14 / (6,67 10^-11*2,54 10⁷) =3*3,14/(6,67*2,54) =5,56 10³ kg m^-3.

Calculer la masse volumique r' de la lune sachant que 8T'=9T avec T' période de révolution autour de la lune.

r'=3p/(GT'²)

T'²=81/64 T²

r'=3p/(GT²)*64/81 = r*64/81.

r'=5,56 10³*64/81 = 4,4 10³ kg m^-3.