|
concours
électroradiologie médicale
condensateur :
charge, générateur de courant ou de tension,
décharge à travers un moteur.
Tours
2007
|
|||||||||||||||||||
|
|||||||||||||||||||
|
Quelle est la charge portée par chaque armature au bout de 10 s de charge ? B. On réalise le montage ci-dessous E= 12 V :
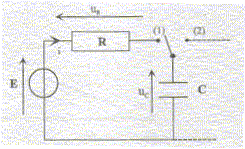
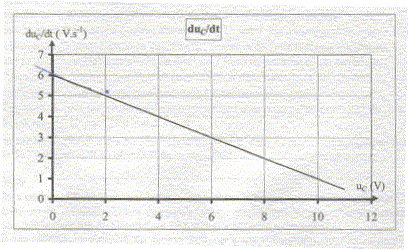
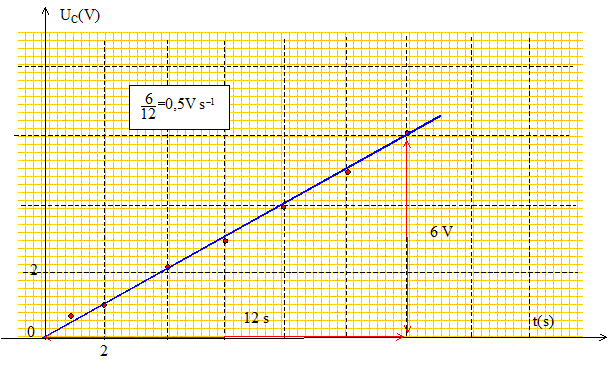
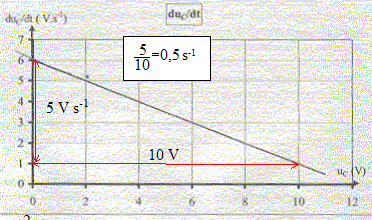
A l'instant t=0 on ferme l'interrupteur K en position (1), le condensateur étant totalement déchargé, et on relève les valeurs de uC en fonction du temps. Etablir la relation entre E, uC et uR. Exprimer les relations existant entre uR, R et i, et entre i, C et la dérivée de uC par rapport au temps. En déduire l'équation différentielle à laquelle obéit uC. Donner l'expression de la constante de temps t et montrer qu'elle est homogène à un temps. Vérifier que uC=E(1-exp(-t/t) est solution de cette équation différentielle. Le système d'aquisition permet de tracer la courbe donnant duC/dt en fonction de uC.
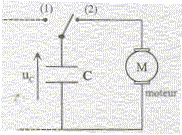
Que représente le coefficient directeur de la droite ? Justifier. En déduire t. Que vaut la capacité du condensateur si R= 10 kW ? C. Le condensateur étant chargé sous la tension de 12 V, on bascule rapidement l'interrupteur en position (2). Il se décharge dans un moteur qui peut faire monter une petite masse m= 10,0 g.
Donner les expressions de l'énergie de ce condensateur chargé puis l'évaluer. Déterminer l'énergie fournie à la masse m pour la soulever d'une hauteur h. Le moteur cesse de fonctionner lorsque la tension uC vaut 4,0 V. Trouver la hauteur maximale dont la masse peut s'élever. g= 10 m/s² ; 122 = 144 ;
Capacité du condensateur : Q= It et Q= CuC d'où uC = I/C t avec I= 10-4 A. uC = 10-4 /C t Le coefficient directeur de la droite vaut : 10-4 /C = 0,5 V /s ; C= 10-4 / 0,5 ; C=2 10-4 F. Charge portée par chaque armature au bout de 10 s de charge : Q= It = 10-4 *10 ; Q= 10-3 C. ( coulomb) L'armature relié à la borne + du générateur porte la charge + 10-3 C; celle reliée à la borne - du générateur porte la charge -10-3 C. B. On réalise le montage ci-dessous E= 12 V :
Relation entre E, uC et uR. Additivité des tensions : E= uR+uC. Avec uR=R i, et q =CuC ; de plus i = dq/dt = CduC/dt Equation différentielle à laquelle obéit uC. E= RCduC/dt + uC. (1) La constante de temps t est égale à t =RC. Montrons que RC est homogène à un temps : R : tension / intensité ; C : charge / tension soit intensité * temps / tension. RC : temps ou encore [RC] = T. Vérifions que uC=E(1-exp(-t/t) est solution de cette équation différentielle. dériver duC/dt = E/t exp(-t/t) = E/(RC) exp(-t/t) Repport dans (1) : E= E exp(-t/t) + E(1-exp(-t/t) Cette égalité étant vérifiée quel que soit le temps, uC=E(1-exp(-t/t) est bien solution de l'équation différentielle.
(1) s'écrit : duC/dt =E /(RC) -1/(RC) uC. Le coefficient directeur de la droite est égal à 1/t = 0,5 s-1. t = 1/0,5 = 2 s. Capacité du condensateur si R= 10 kW : t =RC soit C= t /R = 2 / 104 ; C= 2 10-4 F.
Le condensateur étant chargé sous la tension de 12 V, on bascule rapidement l'interrupteur en position (2). Il se décharge dans un moteur qui peut faire monter une petite masse m= 10,0 g.
Energie de ce condensateur chargé : ½CE2 = 0,5 * 2 10-4 * 122 = 1,44 10-2 J. Energie fournie à la masse m pour la soulever d'une hauteur h. C'est l'opposé du travail du poids soit : m g h. Hauteur maximale dont la masse peut s'élever. Le moteur cesse de fonctionner lorsque la tension uC vaut 4,0 V. Energie résiduelle dans le condensateur : ½C uC2 = 0,5*2 10-4 * 42 = 1,6 10-3 J Energie fournie au moteur : 1,44 10-2 - 1,6 10-3 = 1,28 10-2 J. Dans l'hypothèse d'un rendement de 100 % : 1,28 10-2 = mg h h = 1,28 10-2 /( mg) = 1,28 10-2 /(0,01*10) ; h = 0,128 m.
|
|||||||||||||||||||
|
|